题目内容
4.求证:$\frac{1+2sinθcosθ}{co{s}^{2}θ-si{n}^{2}θ}$=$\frac{1+tanθ}{1-tanθ}$.分析 把左边分子化为完全平方式,分母展开平方差公式,约分后化弦为切得答案.
解答 证明:$\frac{1+2sinθcosθ}{co{s}^{2}θ-si{n}^{2}θ}$
=$\frac{(sinθ+cosθ)^{2}}{(cosθ+sinθ)(cosθ-sinθ)}$
=$\frac{sinθ+cosθ}{cosθ-sinθ}$
=$\frac{1+tanθ}{1-tanθ}$.
点评 本题考查三角恒等式的证明,考查同角三角函数的基本关系式,是基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.已知O为坐标原点,实数x,y满足$\left\{\begin{array}{l}{x-y+1≤0}\\{3x+4y≤12}\\{x-1≥0}\end{array}\right.$,P(x,y)为该不等式组所表示的平面区域内任意一点,使z=x+2y取最大值的点为A点,则|OP|•|AO|•cos∠AOP的最大值等于( )
| A. | $\frac{97}{16}$ | B. | $\frac{11}{2}$ | C. | $\frac{167}{28}$ | D. | $\frac{38}{7}$ |
13.实数x,y,z满足x2-2x+y=z-1且x+y2+1=0,则x,y,z满足的下列关系式为( )
| A. | z≥y>x | B. | z≥x>y | C. | x>z≥y | D. | z>x≥y |
18.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,则不等式f(2x+3)≤5的解集为( )
| A. | [-5,5] | B. | [-8,2] | C. | [-4,1] | D. | [1,4] |
 如图,空间四边形ABCD的每条边和AC,BD的长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.
如图,空间四边形ABCD的每条边和AC,BD的长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.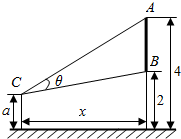 如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.