题目内容
已知函数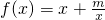 ,且f(1)=2
,且f(1)=2
(1)判断f(x)的奇偶性,并证明;
(2)判断f(x)在(1,+∞)上的单调性,并证明;
(3)若f(a)>2,求a的取值范围.
解:∵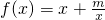 ,且f(1)=2
,且f(1)=2
∴1+m=2,解得 m=1…
(1)y=f(x)为奇函数,理由如下:
∵ ,定义域为(-∞,0)∪(0,+∞),关于原点对称.
,定义域为(-∞,0)∪(0,+∞),关于原点对称.
又
所以y=f(x)为奇函数
(2)f(x)在(1,+∞)上的单调递增,理由如下.
设1<x1<x2,
则
∵1<x1<x2
∴x2-x1>0,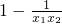 >0
>0
故f(x2)-f(x1)>0,即f(x2)>f(x1),f(x)在(1,+∞)上的单调递增
(3)若f(a)>2,
即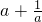 >2,显然a>0
>2,显然a>0
则原不等式可化为a2-2a+1=(a-1)2>0
解得a>0且a≠1
分析:(1)由已知中f(1)=2,代入可得m的值,进而求出函数的解析式,根据函数奇偶性的定义判断f(-x)与f(x)的关系,可得函数的奇偶性
(2)任取1<x1<x2,判断f(x2)与f(x1)的大小,进而根据函数单调性的定义,可得函数的单调性
(3)由(1)中所得函数的解析式,构造关于a的不等式,解不等式可得答案.
点评:本题考查的知识点是函数的奇偶性,函数的单调性,熟练掌握函数奇偶性与单调性的定义是解答的关键.
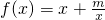 ,且f(1)=2
,且f(1)=2∴1+m=2,解得 m=1…
(1)y=f(x)为奇函数,理由如下:
∵
 ,定义域为(-∞,0)∪(0,+∞),关于原点对称.
,定义域为(-∞,0)∪(0,+∞),关于原点对称.又

所以y=f(x)为奇函数
(2)f(x)在(1,+∞)上的单调递增,理由如下.
设1<x1<x2,
则

∵1<x1<x2
∴x2-x1>0,
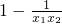 >0
>0故f(x2)-f(x1)>0,即f(x2)>f(x1),f(x)在(1,+∞)上的单调递增
(3)若f(a)>2,
即
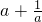 >2,显然a>0
>2,显然a>0则原不等式可化为a2-2a+1=(a-1)2>0
解得a>0且a≠1
分析:(1)由已知中f(1)=2,代入可得m的值,进而求出函数的解析式,根据函数奇偶性的定义判断f(-x)与f(x)的关系,可得函数的奇偶性
(2)任取1<x1<x2,判断f(x2)与f(x1)的大小,进而根据函数单调性的定义,可得函数的单调性
(3)由(1)中所得函数的解析式,构造关于a的不等式,解不等式可得答案.
点评:本题考查的知识点是函数的奇偶性,函数的单调性,熟练掌握函数奇偶性与单调性的定义是解答的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 ,且f(1)=log162,f(-2)=1.
,且f(1)=log162,f(-2)=1. ,且f(1)=2,
,且f(1)=2,
 ,且f(1)=2,
,且f(1)=2,
 ,且f(1)=1,f(-2)=4.
,且f(1)=1,f(-2)=4. 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ,且f(1)=3
,且f(1)=3