题目内容

设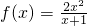 $数学公式$ ，g（x）=ax+5-2a（a＞0），若对于任意x₁∈[0，1]，总存在x₀∈[0，1]，使得g（x₀）=f（x₁）成立，则a的取值范围是________．

$\text{[math]}$ ≤a≤4
分析：先对函数f（x）分x=0和x≠0分别求函数值，综合可得其值域，同样求出函数g（x）的值域，把两个函数的函数值相比较即可求出a的取值范围．
解答：∵ $\text{[math]}$ ，
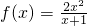当x=0时，f（x）=0，
当x≠0时，f（x）= $\text{[math]}$ = $\text{[math]}$ ，
由0＜x≤1，∴0＜f（x）≤1．
故0≤f（x）≤1
又因为g（x）=ax+5-2a（a＞0），且g（0）=5-2a，g（1）=5-a．
故5-2a≤g（x）≤5-a．
所以须满足 $\text{[math]}$ ，
∴ $\text{[math]}$ ≤a≤4，
故答案为 $\text{[math]}$ ≤a≤4．
点评：本题主要考查函数恒成立问题以及函数值域的求法，是对知识点的综合考查，属于基础题．

练习册系列答案

期末复习检测系列答案

超能学典单元期中期末专题冲刺100分系列答案

期末100分冲刺卷系列答案

黄冈360度定制密卷系列答案

聚能闯关期末复习冲刺卷系列答案

同步测试卷过关冲刺100分系列答案

阳光考场单元测试卷系列答案

给力闯关100分系列答案

名校联盟冲刺卷系列答案

精英教程全能卷系列答案

相关题目

已知函数f(x)=

，x∈[-2，-1)

-2，x∈[-1，

（1）求f（x）的值域；
（2）设函数g（x）=ax-2，x∈[-2，2]，对于任意x₁∈[-2，2]，总存在x₀∈[-2，2]，使得g（x₀）=f（x₁）成立，求实数a的取值范围．

已知函数f（x）=

（m，n∈R）在x=1处取到极值2
（Ⅰ）求f（x）的解析式；
（Ⅱ）设函数g（x）=ax-lnx．若对任意的x1∈[

，2]，总存在唯一的x2∈[

]，使得g（x₂）=f（x₁），求实数a的取值范围．

已知函数f（x）=a（x-

）-lnx，x∈R．
（1）若a=2，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若a＞0，求函数f（x）的单调区间；
（3）设函数g（x）=-

．若至少存在一个x₀∈[1，+∞），使得f（x₀）＞g（x₀）成立，求实数a的取值范围．

已知函数f（x）=

（m，n∈R）在x=1处取到极值2．
（1）求f（x）的解析式；
（2）设函数g（x）=ax-lnx．若对任意的x₁∈[

，2]，总存在唯一的x₂∈[

，e]（e为自然对数的底），使得g（x₂）=f（x₁），求实数a的取值范围．

已知函数f(x)=

，x∈[-2，-1)

-2，x∈[-1，

（1）判断当x∈[-2，1）时，函数f（x）的单调性，并用定义证明之；
（2）求f（x）的值域
（3）设函数g（x）=ax-2，x∈[-2，2]，若对于任意x₁∈[-2，2]，总存在x₀∈[-2，2]，使g（x₀）=f（x₁）成立，求实数a的取值范围．