题目内容
定义在R上的函数f(x)满足f(x)=f(3-x),且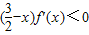 ,已知x1<x2,x1+x2<3,则( )
,已知x1<x2,x1+x2<3,则( )A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)+f(x2)<0
D.f(x1)+f(x2)>0
【答案】分析:由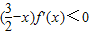 可判断f(x)的单调性,由x1<x2,x1+x2<3可分x1<x2<
可判断f(x)的单调性,由x1<x2,x1+x2<3可分x1<x2< 及x1<
及x1< <x2两种情况进行讨论,借助单调性可作出判断.
<x2两种情况进行讨论,借助单调性可作出判断.
解答:解:由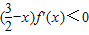 得,
得,
当x< 时,f′(x)<0,f(x)递减;当x>
时,f′(x)<0,f(x)递减;当x> 时,f′(x)>0,f(x)递增;
时,f′(x)>0,f(x)递增;
因为x1<x2,x1+x2<3,
所以x1<x2< 时,f(x)递减,f(x1)>f(x2);
时,f(x)递减,f(x1)>f(x2);
当x1< <x2时,3-x1>
<x2时,3-x1> ,且3-x1>x2,f(x)在(
,且3-x1>x2,f(x)在( ,+∞)上递增,
,+∞)上递增,
所以f(3-x1)=f(x1)>f(x2);
综上,f(x1)>f(x2),
故选B.
点评:本题考查函数的单调性及其应用,考查导数与单调性的关系,考查学生推理论证能力.
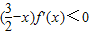 可判断f(x)的单调性,由x1<x2,x1+x2<3可分x1<x2<
可判断f(x)的单调性,由x1<x2,x1+x2<3可分x1<x2< 及x1<
及x1< <x2两种情况进行讨论,借助单调性可作出判断.
<x2两种情况进行讨论,借助单调性可作出判断.解答:解:由
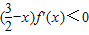 得,
得,当x<
 时,f′(x)<0,f(x)递减;当x>
时,f′(x)<0,f(x)递减;当x> 时,f′(x)>0,f(x)递增;
时,f′(x)>0,f(x)递增;因为x1<x2,x1+x2<3,
所以x1<x2<
 时,f(x)递减,f(x1)>f(x2);
时,f(x)递减,f(x1)>f(x2);当x1<
 <x2时,3-x1>
<x2时,3-x1> ,且3-x1>x2,f(x)在(
,且3-x1>x2,f(x)在( ,+∞)上递增,
,+∞)上递增,所以f(3-x1)=f(x1)>f(x2);
综上,f(x1)>f(x2),
故选B.
点评:本题考查函数的单调性及其应用,考查导数与单调性的关系,考查学生推理论证能力.

练习册系列答案
相关题目