Question

已知函数f（x）=

1

3

x3+

1

2

ax2+2bx+c在R上可导．
（1）若f（x）在区间[-1，2]上为减函数，且b=3a，求a的取值范围；
（2）若f（x）的极大值点在（0，1）内，极小值点在（1，2）内，求

b-2

a-1

的取值范围．

Answer 1

分析：（1）由f（x）在区间[-1，2]上为减函数，可转化成f'（x）≤0对x∈[-1，2]恒成立，借助二次函数的知识建立不等关系，可求出a的取值范围．
（2）对函数f（x）求导，根据函数f（x）在（0，1）内有极大值，在（1，2）内有极小值，转化为f′（x）的图象在区间（0，1）和（1，2）上与x轴各有一个交点，根据二次函数根的分布可建立关于a，b的三个不等关系，利用线性规划即可求

b-2

a-1

的取值范围．

解答：（1）∵当a≠0时，f′（x）=x²+ax+2b=x²+ax+6a，又f（x）在[-1，2]上为减函数，
∴f′（x）≤0对x∈[-1，2]恒成立，…（2分）
即x²+ax+6a≤0对x∈[-1，2]恒成立，
∴f′（-1）≤0且f′（2）≤0，…（4分）
即

1-a+6a≤0 4+2a+6a≤0

⇒

a≤- 1 5 a≤- 1 2

⇒a≤-

1

2

．…（6分）
（2）∵f（x）=

1

3

x³+

1

2

ax²+2bx+c，
∴f′（x）=x²+ax+2b，…（8分）
由题意得

f′(0)=2b＞0 f′(1)=1+a+2b＜0 f′(2)=4+2a+2b＞0

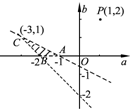
画出可行域：
于是

b-2

a-1

即为点P（1，2）与可行域内（不包含边界）任意一点的连线的斜率．
∴k_PC＜

b-2

a-1

＜k_PA，即

1

4

＜

b-2

a-1

＜1．…（13分）

点评：本小题主要考查函数的导数，单调性，极值，不等式等基础知识，考查综合利用数学知识分析问题、解决问题的能力，属于中档题．