Question

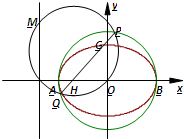已知圆O：x²+y²=8交x轴于A，B两点，曲线C是以AB为长轴，直线l：x=-4为准线的椭圆．
（1）求椭圆的标准方程；
（2）若M是直线l上的任意一点，以OM为直径的圆K与圆O相交于P，Q两点，求证：直线PQ必过定点E，并求出点E的坐标．

Answer 1

分析：（1）因为A，B两点是圆O：x²+y²=8与x轴的交点，所以坐标可知，椭圆的长轴长也就可知，a就能求出，再根据x=-4为椭圆准线，得到c值，再用a，b，c的关系式求出b值即可．
（2）先根据M点的坐标设出以OM为直径的圆K的方程，与圆O方程联立，消去x²，y²，在判断所得的直线方程是否过定点即可．

解答：解：（1）设椭圆的标准方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，则：

a=2 2 a2 c =4

，从而：

a=2 2 c=2

，故b=2，所以椭圆的标准方程为

x2

8

+

y2

4

=1．
（2）设M（-4，m），则圆K方程为(x+2)2+(y-

m

2

)2=

m2

4

+4与圆O：x²+y²=8联立消去x²，y²得PQ的方程为4x-my+8=0，过定点E（-2，0）

点评：本题考查了椭圆方程的求法，以及圆与圆位置关系的判断，属于圆锥曲线与圆的综合题．