题目内容
已知函数f(x)= (x≥0).
(x≥0).(1)若f(x)>0恒成立,求实数k的取值范围;
(2)若对任意非负实数a,b,c,以f(a),f(b),f(c)为三边都可构成三角形,求实数k的取值范围.
【答案】分析:(1)f(x)>0恒成立等价于x2+kx+1>0(x≥0)恒成立.x=0时,结论成立;x>0时,分离参数-k<x+ ,利用基本不等式,即可确定实数k的取值范围;
,利用基本不等式,即可确定实数k的取值范围;
(2)f(x)= ,由(1)知:k>-2,再进行分类讨论,利用以f(a),f(b),f(c)为三边都可构成三角形,即可求实数k的取值范围.
,由(1)知:k>-2,再进行分类讨论,利用以f(a),f(b),f(c)为三边都可构成三角形,即可求实数k的取值范围.
解答:解:(1)∵x2+x+1>0恒成立,∴f(x)>0恒成立等价于x2+kx+1>0(x≥0)恒成立
x=0时,结论成立;x>0时,-k<x+ ,∵x>0,∴x+
,∵x>0,∴x+ ≥2
≥2
∴-k<2
∴k>-2
(2)f(x)=
由(1)知:k>-2
1°、当k=1时,满足题意;
2°、当k>1时, ,由题意知:
,由题意知: ,∴1<k<4
,∴1<k<4
3°、当k<1时,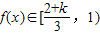 ,于是有
,于是有 ,∴1>
,∴1>
综上,实数k的取值范围为 .
.
点评:本题考查恒成立问题,考查分类讨论的数学思想,解题的关键是正确分类,属于中档题.
 ,利用基本不等式,即可确定实数k的取值范围;
,利用基本不等式,即可确定实数k的取值范围;(2)f(x)=
 ,由(1)知:k>-2,再进行分类讨论,利用以f(a),f(b),f(c)为三边都可构成三角形,即可求实数k的取值范围.
,由(1)知:k>-2,再进行分类讨论,利用以f(a),f(b),f(c)为三边都可构成三角形,即可求实数k的取值范围.解答:解:(1)∵x2+x+1>0恒成立,∴f(x)>0恒成立等价于x2+kx+1>0(x≥0)恒成立
x=0时,结论成立;x>0时,-k<x+
 ,∵x>0,∴x+
,∵x>0,∴x+ ≥2
≥2∴-k<2
∴k>-2
(2)f(x)=

由(1)知:k>-2
1°、当k=1时,满足题意;
2°、当k>1时,
 ,由题意知:
,由题意知: ,∴1<k<4
,∴1<k<43°、当k<1时,
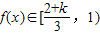 ,于是有
,于是有 ,∴1>
,∴1>
综上,实数k的取值范围为
 .
.点评:本题考查恒成立问题,考查分类讨论的数学思想,解题的关键是正确分类,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|