题目内容
(5分)(2011•福建)若关于x的方程x2+mx+1=0有两个不相等的实数根,则实数m的取值范围是( )
| A.(﹣1,1) | B.(﹣2,2) | C.(﹣∞,﹣2)∪(2,+∞) | D.(﹣∞,﹣1)∪(1,+∞) |
C
解析试题分析:利用题中条件:“关于x的方程x2+mx+1=0有两个不相等的实数根”由韦达定理的出m的关系式,解不等式即可.
解:∵关于x的方程x2+mx+1=0有两个不相等的实数根,
∴△>0,
即:m2﹣4>0,
解得:m∈(﹣∞,﹣2)∪(2,+∞).
故选C.
点评:本题考查一元二次方程的根的判别式与根的关系,属于基本运算的考查.

练习册系列答案
相关题目
(5分)(2011•天津)对实数a与b,定义新运算“?”:a?b= .设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
| A.(﹣1,1]∪(2,+∞) | B.(﹣2,﹣1]∪(1,2] | C.(﹣∞,﹣2)∪(1,2] | D.[﹣2,﹣1] |
对任意实数 ,
, 定义运算“⊙”:
定义运算“⊙”: 设
设 ,若函数
,若函数 的图象与
的图象与 轴恰有三个交点,则
轴恰有三个交点,则 的取值范围是( )
的取值范围是( )
A.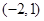 | B. |
C. | D.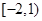 |
函数y=ln(x+1)与 的图像交点的横坐标所在区间为( )
的图像交点的横坐标所在区间为( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
已知函数f(x)的图象如图所示,则f(x)的解析式可以是( )
A.f(x)= |
B.f(x)= |
C.f(x)=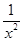 -1 -1 |
D.f(x)=x- |

 的最大值为( )
的最大值为( )
| A.0 | B.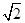 | C.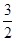 | D. |
[2014·武汉模拟]函数f(x)= 的值域为( )
的值域为( )
| A.(-∞,-1) |
| B.(-1,0)∪(0,+∞) |
| C.(-1,+∞) |
| D.(-∞,-1)∪(0,+∞) |
 (a≠0)在同一坐标系中的图象可能是( )
(a≠0)在同一坐标系中的图象可能是( )
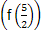 的值是( )
的值是( )
