题目内容
函数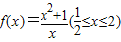 的值域为 .
的值域为 .
【答案】分析:由f(x)=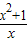 =
=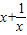 在[
在[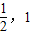 ]上单调递减,在[1,2]上单调递增,结合函数的单调性即可求解函数的最值
]上单调递减,在[1,2]上单调递增,结合函数的单调性即可求解函数的最值
解答:解:∵f(x)=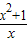 =
=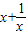 在[
在[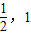 ]上单调递减,在[1,2]上单调递增
]上单调递减,在[1,2]上单调递增
∴当x=1时,函数有最小值f(1)=2
∵f(2)= ,
,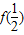 =
=
∴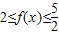
故答案为:[2, ]
]
点评:本题主要考查了函数的单调性在求解函数的最值中的应用,属于基础试题
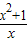 =
=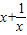 在[
在[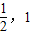 ]上单调递减,在[1,2]上单调递增,结合函数的单调性即可求解函数的最值
]上单调递减,在[1,2]上单调递增,结合函数的单调性即可求解函数的最值解答:解:∵f(x)=
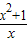 =
=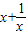 在[
在[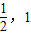 ]上单调递减,在[1,2]上单调递增
]上单调递减,在[1,2]上单调递增∴当x=1时,函数有最小值f(1)=2
∵f(2)=
 ,
,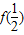 =
=
∴
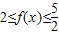
故答案为:[2,
 ]
]点评:本题主要考查了函数的单调性在求解函数的最值中的应用,属于基础试题

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题: