题目内容

在下列关于函数y=
3
sin2x+cos2x的结论中，正确的是（　　）
A．在区间[-
π
3
+kπ，
π
6
+kπ]（k∈Z）上是增函数
B．周期是
π
2
C．最大值为1，最小值为-1
D．是奇函数
∵y=
3
sin2x+cos2x=2sin（2x+
π
6
），令-
1
2
π+2kπ≤2x+
π
6
≤
1
2
π+2kπ，k∈Z
可得-
1
3
π+kπ≤x≤
1
6
π+kπ
即函数的单调递增区间为：[-
1
3
π+kπ，
1
6
π+kπ]
由周期公式可得T=π，函数的最大值为2，最小值为-2，非奇非偶函数
故选：A
练习册系列答案
相关题目
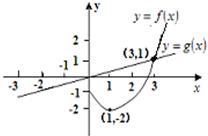精英家教网对于任意的实数a，b，记max{a，b}=
a(a≥b)
b(a＜b)
．若F（x）=max{f（x），g（x）}（x∈R），其中函数  y=f（x）（x∈R）是奇函数，且当x≥0时，f（x）=（x-1）2-2；函数y=g（x）（x∈R）是正比例函数，其图象与x≥0时函数y=f（x）的图象如图所示，则下列关于函数y=F（x）的说法中，正确的是（　　）
A、y=F（x）为奇函数
B、y=F（x）在（-3，0）上为增函数
C、y=F（x）的最小值为-2，最大值为2
D、以上说法都不正确
对于任意的实数a、b，记max{a，b}=
a(a≥b)
b(a＜b)
．若F（x）=max{f（x），g（x）}（x∈R），其中函数y=f（x）（x∈R）是奇函数，且在x=1处取得极小值-2，函数y=g（x） （x∈R）是正比例函数，其图象与x≥0时的函数y=f（x）的图象如图所示，则下列关于函数y=F（x）的说法中，正确的是（　　）
对于任意的实数a、b，记max{a，b}=
a(a≥b)
b(a＜b)
．设F（x）=max{f（x），g（x）}（x∈R），其中g（x）=
1
3
x，y=f（x）是奇函数．当x≥0时，y=f（x）的图象与g（x）的图象如图所示．则下列关于函数y=F（x）的说法中，正确的是（　　）
在下列关于函数y=
3
sin2x+cos2x的结论中，正确的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网