Question

【题目】设、分别是椭圆的左、右焦点.

（1）若是该椭圆上的一个动点，求的最大值；

（2）设过定点的直线与椭圆交于不同的两点、，且为锐角（其中为坐标原点），求直线的斜率的取值范围.

Answer 1

【答案】（1）的最大值；（2）斜率的取值范围为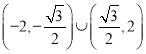

【解析】

（1）设P（x，y），向量坐标化得x2+y2﹣3．由此能够求出向量乘积的取值范围．

（2）设直线l：y＝kx﹣2，M（x1，y1），B（x2，y2），联立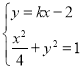，得：，由韦达定理和根的判别式知：或k，又0°＜∠AOB＜90°cos∠AOB＞00，由此能求出直线l的斜率k的取值范围．

（1）根据题意易知，所以，

设P（x，y），则

x2+y2﹣3

．因为

故﹣2．

（2）显然直线x＝0不满足题设条件，

故设直线l：y＝kx+2，M（x1，y1），B（x2，y2），

联立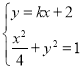，消去y，整理得：，

∴，

由，

得：或k，

又0°＜∠AOB＜90°cos∠AOB＞00，∴x1x2+y1y2＞0，

又y1y2＝（kx1+2）（kx2+2）＝k2x1x2+2k（x1+x2）+4

．

∵，

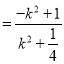即k2＜4，∴﹣2＜k＜2．

故由①、②得，或．