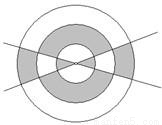
题目内容
 如图三同心圆,其半径分别为3、2、1.已知图中阴影区域的面积是非阴影区域面积的
如图三同心圆,其半径分别为3、2、1.已知图中阴影区域的面积是非阴影区域面积的| 8 | 13 |
分析:首先把三个圆分别分析,第一个为圆,第二个为半径2与半径1的同心圆的圆环,第三个为半径3与半径2的同心圆的圆环.分别求出阴影部分的面积.然后通过已知阴影区域的面积占总面积的
,求出阴影部分面积.两个面积相同,即可解除答案
| 8 |
| 21 |
解答:解:设两直线所夹锐角的弧度为 α
根据题意,
对于第一个圆,阴影部分面积:
•π=α
对于第一个圆,阴影部分面积:
•(4π-π)=3π-3α
对于第一个圆,阴影部分面积:
•(9π-4π)=5α
所有阴影部分面积之和:α+3π-3α+5α=3π+3α ①
而根据已知图中阴影区域的面积是非阴影区域面积的
可得:阴影区域的面积占总面积的
即阴影区域的面积 9π×
②
由①②相等可得:3π+3α=9π×
解得:α=
故答案为:
.
根据题意,
对于第一个圆,阴影部分面积:
| α |
| π |
对于第一个圆,阴影部分面积:
| π-α |
| π |
对于第一个圆,阴影部分面积:
| α |
| π |
所有阴影部分面积之和:α+3π-3α+5α=3π+3α ①
而根据已知图中阴影区域的面积是非阴影区域面积的
| 8 |
| 13 |
可得:阴影区域的面积占总面积的
| 8 |
| 21 |
即阴影区域的面积 9π×
| 8 |
| 21 |
由①②相等可得:3π+3α=9π×
| 8 |
| 21 |
解得:α=
| π |
| 7 |
故答案为:
| π |
| 7 |
点评:本题考查两直线夹角问题,实际上为考查几何概型.通过对三个同心圆的考查,通过两种途径求出阴影部分的面积,继而可以求出夹角.属于难题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 地面上有三个同心圆(如图),其半径分别为3、2、1.若向图中最大的圆内投点且投到图中阴影区域的概率为
地面上有三个同心圆(如图),其半径分别为3、2、1.若向图中最大的圆内投点且投到图中阴影区域的概率为
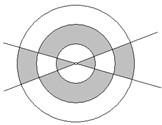 如图三同心圆,其半径分别为3、2、1.已知图中阴影区域的面积是非阴影区域面积的
如图三同心圆,其半径分别为3、2、1.已知图中阴影区域的面积是非阴影区域面积的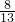 .则两直线所夹锐角的弧度为 ________.
.则两直线所夹锐角的弧度为 ________.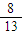 .则两直线所夹锐角的弧度为 .
.则两直线所夹锐角的弧度为 .