题目内容
已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)<f(x)g′(x),f(x)=axg(x),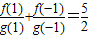 ,在有穷数列{
,在有穷数列{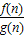 }(n=1,2,…,10)中,任意取前k项相加,则前k项和大于
}(n=1,2,…,10)中,任意取前k项相加,则前k项和大于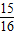 的概率是( )
的概率是( )A.

B.

C.

D.

【答案】分析:令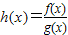 ,由题意可知0<a<1,由
,由题意可知0<a<1,由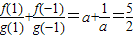 ,可知
,可知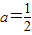 ,由此可知Sn的表达式,由
,由此可知Sn的表达式,由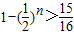 ,得n>4,由此能够求出前k项和大于
,得n>4,由此能够求出前k项和大于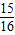 的概率.
的概率.
解答:解:令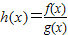 ,
,
则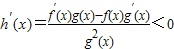 ,
,
故h(x)=ax单调递减,
所以0<a<1,
又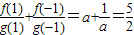 ,
,
解得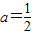 ,
,
则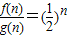 ,
,
其前n项和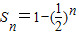 ,
,
由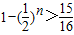 ,得n>4,
,得n>4,
故所求概率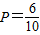 =
= .
.
故选D.
点评:本题考查概率的求法和导数的性质,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答,注意概率计算公式的灵活运用.
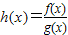 ,由题意可知0<a<1,由
,由题意可知0<a<1,由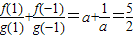 ,可知
,可知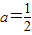 ,由此可知Sn的表达式,由
,由此可知Sn的表达式,由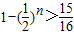 ,得n>4,由此能够求出前k项和大于
,得n>4,由此能够求出前k项和大于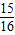 的概率.
的概率.解答:解:令
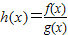 ,
,则
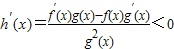 ,
,故h(x)=ax单调递减,
所以0<a<1,
又
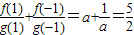 ,
,解得
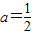 ,
,则
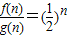 ,
,其前n项和
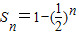 ,
,由
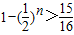 ,得n>4,
,得n>4,故所求概率
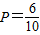 =
= .
.故选D.
点评:本题考查概率的求法和导数的性质,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答,注意概率计算公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目