题目内容
已知数列{an}是等差数列,bn=![]() ,b1+b2+b3=
,b1+b2+b3=![]() ,b1b2b3=
,b1b2b3=![]() ,求an.
,求an.
an=2n-3或an=5-2n.
解析:
设an=a1+(n-1)d,由b1b2b3=(![]()
![]() =(
=(![]()
![]() =
=![]() 知a2=1.
知a2=1.
故b1+b3=![]() ,
,
b1b3=![]() =
=![]() .
.
∴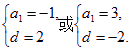
∴an=2n-3或an=5-2n.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
题目内容
已知数列{an}是等差数列,bn=![]() ,b1+b2+b3=
,b1+b2+b3=![]() ,b1b2b3=
,b1b2b3=![]() ,求an.
,求an.
an=2n-3或an=5-2n.
设an=a1+(n-1)d,由b1b2b3=(![]()
![]() =(
=(![]()
![]() =
=![]() 知a2=1.
知a2=1.
故b1+b3=![]() ,
,
b1b3=![]() =
=![]() .
.
∴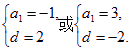
∴an=2n-3或an=5-2n.

 同步轻松练习系列答案
同步轻松练习系列答案