题目内容

已知函数f(x)=ax2+bx+c,当|x|≤1时,|f(x)|≤1,求证:(1)|c|≤1；(2)|b|≤1.

证明:(1)当|x|≤1时,|f(x)|≤1,取x=0,

得|c|=|f(0)|≤1,?

即|c|≤1.?

(2)由|f(1)|≤1,得|a+b+c|≤1,?

由|f(-1)|≤1,得|a-b+c|≤1,?

∴

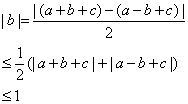
练习册系列答案
相关题目
已知函数f(x)=a-
12x+1
．
（1）求证：不论a为何实数f（x）总是为增函数；
（2）确定a的值，使f（x）为奇函数；
（3）当f（x）为奇函数时，求f（x）的值域．
已知函数f(x)
a-x  ，x≤0
1  ，0＜x≤3
(x-5)2-a，x＞3
（a＞0且a≠1）图象经过点Q（8，6）．
（1）求a的值，并在直线坐标系中画出函数f（x）的大致图象；
（2）求函数f（t）-9的零点；
（3）设q（t）=f（t+1）-f（t）（t∈R），求函数q（t）的单调递增区间．
已知函数f(x)=a-
1
2x+1
，若f（x）为奇函数，则a=（　　）
A、
1
2
B、2
C、
1
3
D、3
已知函数f(x)=
a(x-1)x2
，其中a＞0．
（I）求函数f（x）的单调区间；
（II）若直线x-y-1=0是曲线y=f（x）的切线，求实数a的值；
（III）设g（x）=xlnx-x2f（x），求g（x）在区间[1，e]上的最小值．（其中e为自然对数的底数）
已知函数f(x)=a-
12x-1
，（a∈R）
（1）求f（x）的定义域；
（2）若f（x）为奇函数，求a的值；
（3）考察f（x）在定义域上单调性的情况，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网