题目内容
函数f(x)=x2-ax+b满足f(2013)=f(-2011)且f(0)=3,则f(ax)与f(bx)的大小关系是( )A.f(ax)≥f(bx)
B.f(ax)≤f(bx)
C.f(ax)>f(bx)
D.f(ax)<f(bx)
【答案】分析:先利用二次函数的对称性及f(00=3即可求得a、b的值,然后通过作差再对x分类讨论即可.
解答:解:由f(2013)=f(-2011),说明二次函数f(x)=x2-ax+b的图象关于直线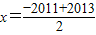 =1对称,
=1对称,
∴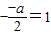 ,解得a=2.
,解得a=2.
又f(0)=3,∴b=3.
∴f(x)=x2-2x+3.
∴f(ax)-f(bx)=f(2x)-f(3x)=(2x-3x)(2x+3x-2),
当x>0时,2x-3x<0,2x+3x-2>0,所以f(ax)<f(bx);
当x=0时,2x-3x=0,2x+3x-2=0,所以f(ax)=f(bx);
当x<0时,2x-3x>0,2x+3x-2<0,所以f(ax)<f(bx);
故f(ax)≤f(bx).
故选B.
点评:熟练掌握二次函数的对称性和指数函数的单调性是解题的关键.
解答:解:由f(2013)=f(-2011),说明二次函数f(x)=x2-ax+b的图象关于直线
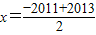 =1对称,
=1对称,∴
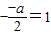 ,解得a=2.
,解得a=2.又f(0)=3,∴b=3.
∴f(x)=x2-2x+3.
∴f(ax)-f(bx)=f(2x)-f(3x)=(2x-3x)(2x+3x-2),
当x>0时,2x-3x<0,2x+3x-2>0,所以f(ax)<f(bx);
当x=0时,2x-3x=0,2x+3x-2=0,所以f(ax)=f(bx);
当x<0时,2x-3x>0,2x+3x-2<0,所以f(ax)<f(bx);
故f(ax)≤f(bx).
故选B.
点评:熟练掌握二次函数的对称性和指数函数的单调性是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目