题目内容
【题目】某企业生产某种产品时的能耗y与产品件数x之间的关系式为y=ax+![]() .且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
.且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
(1)写出函数y关于x的解析式;
(2)用列表法表示此函数,并画出图象.
【答案】(1) ![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)将x=2时,y=100;x=7时,y=35代入解析式,列方程组求出a和b,可写出函数y关于x的解析式;(2)根据定义域列出函数上的各点,在平面直角坐标系中描出这些点,即函数的图象.
试题解析:
(1)将![]()
![]() 代入y=ax+
代入y=ax+![]() 中,
中,
得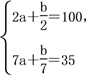
![]()
![]()
所以所求函数解析式为![]() .
.
(2)当x∈{1,2,3,4,5,…,20}时,列表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
y | 197 | 100 | 68.3 | 53 | 44.2 | 38.7 | 35 | 32.5 | 30.8 | 29.6 |
x | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
y | 28.8 | 28.3 | 28.1 | 28 | 28.1 | 28.25 | 28.5 | 28.9 | 29.3 | 29.8 |
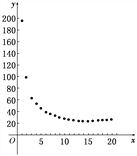
依据上表,画出函数y的图象如图所示,由20个点构成的点列.

练习册系列答案
相关题目
【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
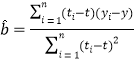 ,
,![]()