题目内容
已知△ABC中,A、B、C分别为三个内角,a、b、c为所对边,2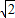 (sin2A-sin2C)=(a-b)sinB,△ABC的外接圆半径为
(sin2A-sin2C)=(a-b)sinB,△ABC的外接圆半径为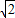 ,
,(1)求角C;
(2)求△ABC面积S的最大值.
【答案】分析:(1)利用正弦定理化简已知等式的右边,整理后再利用余弦定理变形,求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;
(2)由C的度数求出A+B的度数,用A表示出B,利用三角形的面积公式列出关系式,利用正弦定理化简后,将sinC的值及表示出的B代入,利用两角和与差的正弦函数公式化简,整理后利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的图象与性质即可得出面积的最大值.
解答:解:(1)利用正弦定理化简已知的等式得:2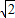 (sin2A-sin2C)=2
(sin2A-sin2C)=2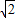 sinB(a-b),
sinB(a-b),
整理得:a2-c2=ab-b2,即a2+b2-c2=ab,
∵c2=a2+b2-2abcosC,即a2+b2-c2=2abcosC,
∴2abcosC=ab,即cosC= ,
,
则C=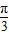 ;
;
(2)∵C=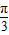 ,∴A+B=
,∴A+B=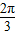 ,即B=
,即B=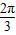 -A,
-A,
∵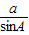 =
=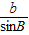 =2
=2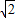 ,即a=2
,即a=2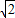 sinA,b=2
sinA,b=2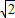 sinB,
sinB,
∴S△ABC= absinC=
absinC= absin
absin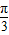 =
= ×2
×2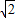 sinA×2
sinA×2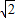 sinB×
sinB×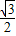
=2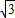 sinAsinB=2
sinAsinB=2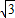 sinAsin(
sinAsin(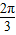 -A)=2
-A)=2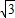 sinA(
sinA(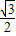 cosA+
cosA+ sinA)
sinA)
=3sinAcosA+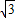 sin2A=
sin2A= sin2A+
sin2A+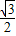 (1-cos2A)
(1-cos2A)
= sin2A-
sin2A-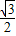 cos2A+
cos2A+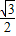 =
=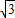 sin(2A-
sin(2A-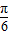 )+
)+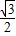 ,
,
则当2A-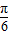 =
=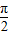 ,即A=
,即A=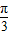 时,S△ABCmax=
时,S△ABCmax=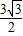 .
.
点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.
(2)由C的度数求出A+B的度数,用A表示出B,利用三角形的面积公式列出关系式,利用正弦定理化简后,将sinC的值及表示出的B代入,利用两角和与差的正弦函数公式化简,整理后利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的图象与性质即可得出面积的最大值.
解答:解:(1)利用正弦定理化简已知的等式得:2
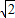 (sin2A-sin2C)=2
(sin2A-sin2C)=2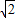 sinB(a-b),
sinB(a-b),整理得:a2-c2=ab-b2,即a2+b2-c2=ab,
∵c2=a2+b2-2abcosC,即a2+b2-c2=2abcosC,
∴2abcosC=ab,即cosC=
 ,
,则C=
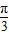 ;
;(2)∵C=
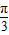 ,∴A+B=
,∴A+B=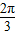 ,即B=
,即B=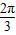 -A,
-A,∵
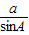 =
=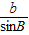 =2
=2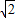 ,即a=2
,即a=2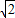 sinA,b=2
sinA,b=2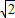 sinB,
sinB,∴S△ABC=
 absinC=
absinC= absin
absin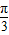 =
= ×2
×2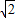 sinA×2
sinA×2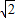 sinB×
sinB×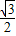
=2
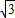 sinAsinB=2
sinAsinB=2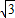 sinAsin(
sinAsin(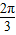 -A)=2
-A)=2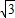 sinA(
sinA(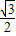 cosA+
cosA+ sinA)
sinA)=3sinAcosA+
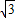 sin2A=
sin2A= sin2A+
sin2A+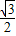 (1-cos2A)
(1-cos2A)=
 sin2A-
sin2A-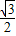 cos2A+
cos2A+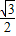 =
=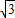 sin(2A-
sin(2A-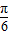 )+
)+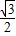 ,
,则当2A-
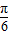 =
=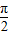 ,即A=
,即A=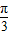 时,S△ABCmax=
时,S△ABCmax=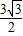 .
.点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目