题目内容
已知数列{an}是各项均不为0的等差数列,公差为d,Sn为其前n项和,且满足 ,n∈N*.数列{bn}满足
,n∈N*.数列{bn}满足 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.
(1)求a1、d和Tn;
(2)若对任意的n∈N*,不等式 恒成立,求实数λ的取值范围.
恒成立,求实数λ的取值范围.
解:(1)∵ ,a1≠0,∴a1=1.….(1分)
,a1≠0,∴a1=1.….(1分)
∵ ,∴(1+d)2=3+3d,
,∴(1+d)2=3+3d,
∴d=-1,2,
当d=-1时,a2=0不满足条件,舍去.
因此d=2.….(4分)
∴an=2n-1,∴ ,∴
,∴ .….(6分)
.….(6分)
(2)当n为偶数时, ,∴
,∴ ,
,
∵ ,当n=2时等号成立,∴
,当n=2时等号成立,∴ 最小值为
最小值为 ,
,
因此 . ….(9分)
. ….(9分)
当n为奇数时, ,
,
∵ 在n≥1时单调递增,∴n=1时
在n≥1时单调递增,∴n=1时 的最小值为
的最小值为 ,∴
,∴ . ….(12分)
. ….(12分)
综上, . ….(14分)
. ….(14分)
分析:(1)利用 ,n取1或2,可求数列的首项与公差,从人体可得数列的通项,进而可求数列的和;
,n取1或2,可求数列的首项与公差,从人体可得数列的通项,进而可求数列的和;
(2)分类讨论,分离参数,求出对应函数的最值,即可求得结论.
点评:本题考查数列的通项与求和,考查恒成立问题,解题的关键是分类讨论,分离参数,属于中档题.
 ,a1≠0,∴a1=1.….(1分)
,a1≠0,∴a1=1.….(1分)∵
 ,∴(1+d)2=3+3d,
,∴(1+d)2=3+3d,∴d=-1,2,
当d=-1时,a2=0不满足条件,舍去.
因此d=2.….(4分)
∴an=2n-1,∴
 ,∴
,∴ .….(6分)
.….(6分)(2)当n为偶数时,
 ,∴
,∴ ,
,∵
 ,当n=2时等号成立,∴
,当n=2时等号成立,∴ 最小值为
最小值为 ,
,因此
 . ….(9分)
. ….(9分)当n为奇数时,
 ,
,∵
 在n≥1时单调递增,∴n=1时
在n≥1时单调递增,∴n=1时 的最小值为
的最小值为 ,∴
,∴ . ….(12分)
. ….(12分)综上,
 . ….(14分)
. ….(14分)分析:(1)利用
 ,n取1或2,可求数列的首项与公差,从人体可得数列的通项,进而可求数列的和;
,n取1或2,可求数列的首项与公差,从人体可得数列的通项,进而可求数列的和;(2)分类讨论,分离参数,求出对应函数的最值,即可求得结论.
点评:本题考查数列的通项与求和,考查恒成立问题,解题的关键是分类讨论,分离参数,属于中档题.

练习册系列答案
相关题目
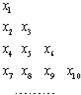 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足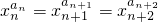 (n∈N*).
(n∈N*).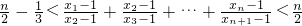 .
. (n∈N*).
(n∈N*). .
.
 (n∈N*).
(n∈N*). .
.