题目内容
已知动圆过定点P(1,0),且与定直线![]() 相切,点C在
相切,点C在![]() 上.
上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-![]() 的直线与曲线M相交于A、B两点,
的直线与曲线M相交于A、B两点,
①求线段AB的长;
②问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(1)y2=4x(2)![]() ;不存在
;不存在
解析:
(1)设M(x,y),依题意有|MP|=|MN|,
所以|x+1|=![]() .化简得:.
.化简得:.
(2)由题意得,直线AB的方程为y=-![]() (x-1).
(x-1).
由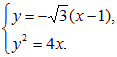 消y得3x2-10x+3=0,
消y得3x2-10x+3=0,
解得x1=![]() ,x2=3. 所以A点坐标为(
,x2=3. 所以A点坐标为(![]() ),B点坐标为(3,-2
),B点坐标为(3,-2![]() ),
),
|AB|=|x1-x2|![]() =
=![]() .假设存在点C(-1,y),使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,即
.假设存在点C(-1,y),使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,即
|
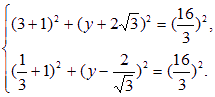
由①-②得42+(y+2![]() )2=(
)2=(![]() )2+(y-
)2+(y-![]() )2,
)2,
解得y=-![]() .但y=-
.但y=-![]() 不符合①,
不符合①,
所以由①,②组成的方程组无解.
因此,直线l上不存在点C,使得△ABC是正三角形.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
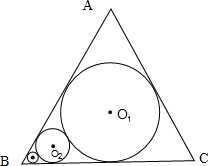 已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.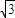 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.