题目内容

设P,Q是边长为a的正方体AC1的面AA1D1D,面A1B1C1D1的中心,如图14,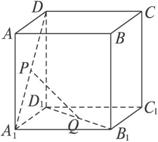

图14

（1）证明PQ∥平面AA1B1B；

（2）求线段PQ的长.

(1)证法一:取AA1,A1B1的中点M,N,连接MN,NQ,MP,

∵MP∥AD,MP=AD,NQ∥A1D1,NQ=A1D1,

∴MP∥ND且MP=ND.

∴四边形PQNM为平行四边形.

∴PQ∥MN.

∵MN面AA1B1B,PQ面AA1B1B,

∴PQ∥面AA1B1B.

证法二:连接AD1,AB1,在△AB1D1中,

显然P,Q分别是AD1,D1B1的中点,

∴PQ∥AB1,且PQ=AB1.

∵PQ面AA1B1B,AB1面AA1B1B,

∴PQ∥面AA1B1B.

(2)解:方法一:PQ=MN==a.

方法二:PQ=AB1=a.

练习册系列答案
相关题目
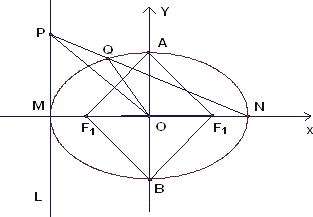精英家教网已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，其左右焦点分别为F1、F2，A、B分别为椭圆的上、下顶点，如果四边形AF1BF2为边长为2的正方形．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设椭圆的左、右顶点为M，N，过点M作x轴的垂线l，在l上任取一点P，连接PN交椭圆C于Q，探究
OP
•
OQ
是否为定值？如果是，求出定值；如果不是，请说明理由．
已知椭圆
y2
a2
+
x2
b2
=1（a＞b＞0）的上下焦点分别为F1，F1，短轴两个端点为P，P1，且四边形F1PF2P1是边长为2的正方形．
（1）求椭圆方程；
（2）设△ABC，AC=2
3
，B为椭圆
y2
a2
+
x2
b2
=1（a＞b＞0）在x轴上方的顶点，当AC在直线y=-1上运动时，求△ABC外接圆的圆心Q的轨迹E的方程；
（3）过点F（0，
3
2
）作互相垂直的直线l1l2，分别交轨迹E于M，N和R，Q．求四边形MRNQ的面积的最小值．
（2012•青岛一模）已知点M在椭圆D：
x2
a2
+
y2
b2
=1（a＞b＞0）上，以M为圆心的圆与x轴相切于椭圆的右焦点，若圆M与y轴相交于A，B两点，且△ABM是边长为
2
6
3
的正三角形．
（Ⅰ）求椭圆D的方程；
（Ⅱ）设P是椭圆D上的一点，过点P的直线l交x轴于点F（-1，0），交y轴于点Q，若
QP
=2
PF
，求直线l的斜率；
（Ⅲ）过点G（0，-2）作直线GK与椭圆N：
3x2
a2
+
4y2
b2
=1左半部分交于H，K两点，又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R，S两点，试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在？请说明理由．
已知点M在椭圆D：
x2
a2
+
y2
b2
=1（a＞b＞0）上，以M为圆心的圆与x轴相切于椭圆的右焦点，若圆M与y轴相交于A，B两点，且△ABM是边长为
2
6
3
的正三角形．
（Ⅰ）求椭圆D的方程；
（Ⅱ）设P是椭圆D上的一点，过点P的直线l交x轴于点F（-1，0），交y轴于点Q，若
QP
=2
PF
，求直线l的斜率；
（Ⅲ）过点G（0，-2）作直线GK与椭圆N：
3x2
a2
+
4y2
b2
=1左半部分交于H，K两点，又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R，S两点，试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网