题目内容
(2013•南京二模)关于x的不等式(2ax-1)lnx≥0对任意x∈(0,+∞)恒成立,则实数a的值为
.
| 1 |
| 2 |
| 1 |
| 2 |
分析:依题意,对x∈(0,1],x∈[1,+∞)分类讨论,构造f(x)=
,利用函数的单调性即可求得实数a的值.
| 1 |
| 2x |
解答:解:∵(2ax-1)lnx≥0对任意x∈(0,+∞)恒成立,
∴当x∈(0,1]时,lnx≤0,
∴2ax-1≤0,
∴a≤
(0<x≤1),
令f(x)=
,则f(x)在(0,1]上单调递减,
∴f(x)min=f(1)=
∴a≤
.①
当x∈[1,+∞)时,lnx≥0,
∴(2ax-1)lnx≥0对任意x∈(0,+∞)恒成立?2ax-1≥0对任意x∈(0,+∞)恒成立,
同理可求a≥f(x)max=f(1)=
.②
由①②得:a=
.
故答案为:
.
∴当x∈(0,1]时,lnx≤0,
∴2ax-1≤0,
∴a≤
| 1 |
| 2x |
令f(x)=
| 1 |
| 2x |
∴f(x)min=f(1)=
| 1 |
| 2 |
∴a≤
| 1 |
| 2 |
当x∈[1,+∞)时,lnx≥0,
∴(2ax-1)lnx≥0对任意x∈(0,+∞)恒成立?2ax-1≥0对任意x∈(0,+∞)恒成立,
同理可求a≥f(x)max=f(1)=
| 1 |
| 2 |
由①②得:a=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查函数恒成立问题,考查构造函数与分类讨论思想,考查函数的单调性,属于难题.

练习册系列答案
相关题目
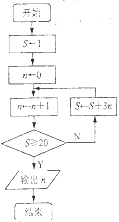 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是