题目内容
【题目】已知常数![]() ,向量
,向量![]() ,
,![]() ,经过定点
,经过定点![]() 且以
且以![]() 为方向向量的直线与经过定点
为方向向量的直线与经过定点![]() 且以
且以![]() 为方向向量的直线交于点
为方向向量的直线交于点![]() ,其中
,其中![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若![]() ,过
,过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意结合直线方向向量的性质可得![]() ,
,![]() ,由平面向量共线的坐标表示可得
,由平面向量共线的坐标表示可得![]() ,
,![]() ,消去
,消去![]() 即可得解;
即可得解;
(2)按照直线![]() 斜率是否存在讨论,当直线斜率存在时,联立方程组,结合韦达定理、平面向量数量积的坐标运算即可得
斜率是否存在讨论,当直线斜率存在时,联立方程组,结合韦达定理、平面向量数量积的坐标运算即可得![]() ,求出取值范围即可得解.
,求出取值范围即可得解.
(1)设![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
由题意![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
消去![]() 得点
得点![]() 轨迹
轨迹![]() 的方程
的方程![]() ;
;
(2)当![]() 时,点
时,点![]() 轨迹方程为
轨迹方程为![]() ,此时
,此时![]() 为双曲线焦点,
为双曲线焦点,
①若直线![]() 斜率不存在,直线
斜率不存在,直线![]() ,不妨设
,不妨设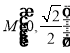 ,
,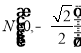
易求得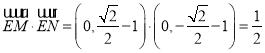 ;
;
②若![]() 斜率存在,设
斜率存在,设![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
则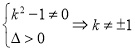 ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]()
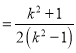
![]() ,
,
由![]() 且
且![]() 可得
可得![]() ,
,
所以![]() ;
;
综上,![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目