题目内容
一自来水厂拟建一座平面图形为矩形、面积为200平方米的净水处理池,该池的深度为1米,池的四周内壁建造单价为每平方米400元,池底建造单价为每平方米60元,在该水池长边的正中间设置一个隔层,将水池分成左右两个小水池,该隔层建造单价为每平方米100元,池壁厚度忽略不计.
(1)净水池的长度设计为多少米时,可使总造价最低?
(2)如长宽都不能超过14.5米,那么此净水池的长为多少时,可使总造价最低?
(1)净水池的长度设计为多少米时,可使总造价最低?
(2)如长宽都不能超过14.5米,那么此净水池的长为多少时,可使总造价最低?
(1)设水池的长为x米,则宽为 米. …………(1分)
米. …………(1分)
总造价:
 …………(4分)
…………(4分)

 …………(6分)
…………(6分)
当且仅当 时,等号成立,
时,等号成立,
故当净水池的长为15米时,总造价最低. ……(7分)
(2)由已知,长不能超过14.5米,而15>14.5,故长度值取不到15,从而不能利用基本不等式求最值,转而考虑利用函数的单调性.
考虑条件 …………(8分)
…………(8分)
设 ,利用函数单调性,
,利用函数单调性,
易知 上为减函数,…………(11分)
上为减函数,…………(11分)
因此,当 时,
时, =36013.8元,故当
=36013.8元,故当 米时,总造价最低. ………(13分)
米时,总造价最低. ………(13分)
 米. …………(1分)
米. …………(1分)总造价:

 …………(4分)
…………(4分)
 …………(6分)
…………(6分)当且仅当
 时,等号成立,
时,等号成立,故当净水池的长为15米时,总造价最低. ……(7分)
(2)由已知,长不能超过14.5米,而15>14.5,故长度值取不到15,从而不能利用基本不等式求最值,转而考虑利用函数的单调性.
考虑条件
 …………(8分)
…………(8分)设
 ,利用函数单调性,
,利用函数单调性,易知
 上为减函数,…………(11分)
上为减函数,…………(11分)因此,当
 时,
时, =36013.8元,故当
=36013.8元,故当 米时,总造价最低. ………(13分)
米时,总造价最低. ………(13分)略

练习册系列答案
相关题目
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形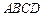 和
和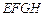 构成的面积为200
构成的面积为200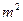 的十字型地域,计划在正方形
的十字型地域,计划在正方形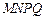 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元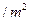 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元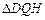 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元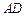 长为
长为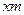 ,
,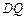 长为
长为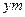 .
.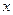 与
与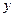 满足的等量关系式;
满足的等量关系式;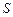 元,试建立
元,试建立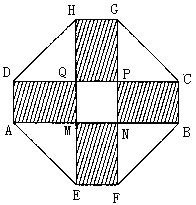
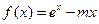
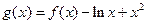 存在两个零点,求m的取值范围;
存在两个零点,求m的取值范围;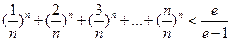 。
。 在(0, 2)内恰有一解, 则实数
在(0, 2)内恰有一解, 则实数 的取值范围为 .
的取值范围为 . ,定义域为D, 若存在
,定义域为D, 若存在 使
使 , 则称
, 则称 为
为 的图象上不动点的坐标为
的图象上不动点的坐标为 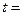 ▲ .
▲ . ,的零点个数为
,的零点个数为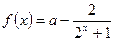 且满足
且满足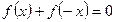 。
。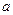 的值;
的值;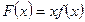 ,判别
,判别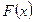 的符号且说明理由;
的符号且说明理由;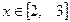 时,关于
时,关于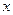 的方程
的方程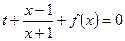 有实数解,求实数
有实数解,求实数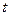 的取值范围。
的取值范围。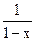 的一个零点.若
的一个零点.若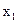 ∈(1,
∈(1,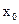 ),
),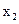 ∈(
∈(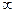 ),则
),则