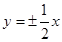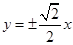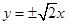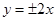题目内容
在平面直角坐标系中,定点 ,两动点
,两动点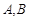 在双曲线
在双曲线 的右支上,则
的右支上,则 的最小值是( )
的最小值是( )
A.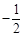 | B.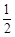 | C. | D. |
D
解析试卷分析:双曲线 右顶点为(
右顶点为( ,0)\过M(1,0)向双曲线引切线,两条切\线所夹的角为符合题意的∠AMB最大角\,切点分别为A,B设切线的斜率为k,切线方程为y=k(x-1)代入
,0)\过M(1,0)向双曲线引切线,两条切\线所夹的角为符合题意的∠AMB最大角\,切点分别为A,B设切线的斜率为k,切线方程为y=k(x-1)代入 ,得
,得 ,
, 整理:
整理: ,设∠AMB=2θ,则∠AMX=θ,tanθ=
,设∠AMB=2θ,则∠AMX=θ,tanθ= =|k|
=|k|
∴tan2θ= ∴sin2θ=
∴sin2θ= ,cos2θ=
,cos2θ= ∴当∠AMB最大时,它的余弦值为
∴当∠AMB最大时,它的余弦值为 .
.
考点:双曲线的性质应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设双曲线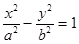
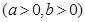 的虚轴长为2,焦距为
的虚轴长为2,焦距为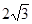 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.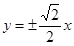 | B.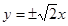 | C.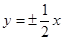 | D. |
设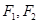 是双曲线
是双曲线 的两个焦点,
的两个焦点,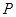 是
是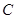 上一点,若
上一点,若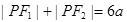 ,且
,且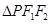 的最小内角为
的最小内角为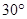 ,则
,则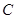 的离心率为( )
的离心率为( )
A.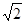 | B.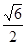 | C.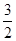 | D.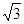 |
双曲线 的渐近线方程是
的渐近线方程是
A. | B. | C. | D. |
双曲线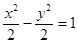 的渐近线方程为( )
的渐近线方程为( )
A.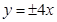 | B.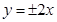 | C.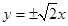 | D.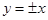 |
抛物线 的焦点到双曲线
的焦点到双曲线 的渐近线的距离是( )
的渐近线的距离是( )
| A.1 | B.2 |
C. | D.2 |
已知圆 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线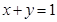 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )
A.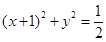 | B.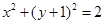 |
C.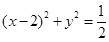 | D. |
过双曲线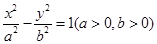 的左焦点
的左焦点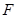 作圆
作圆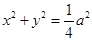 的切线,切点为
的切线,切点为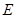 ,直线
,直线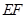 交双曲线右支于点
交双曲线右支于点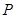 ,若
,若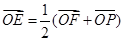 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.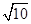 | B.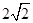 | C.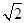 | D.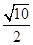 |
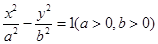 的顶点恰好是椭圆
的顶点恰好是椭圆 的两个顶点,且焦距是
的两个顶点,且焦距是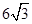 ,则此双曲线的渐近线方程是( )
,则此双曲线的渐近线方程是( )