题目内容
已知定义在R上的奇函数f(x)是(-∞,0]上的增函数,且f(1)=2,f(-2)=-4,设P={x|f(x+t)-4<0},Q={x|f(x)<-2}.若“x∈P”是“x∈Q”的充分不必要条件,则实数t的取值范围是
- A.t≤-1
- B.t>-1
- C.t≥3
- D.t>3
D
分析:根据定义在R上的奇函数f(x)是(-∞,0]上的增函数,且f(1)=2,f(-2)=-4,可以画出f(x)的图象,然后再求出P和Q集合,根据“x∈P”是“x∈Q”的充分不必要条件可得P⊆Q,从而求出t的范围;
解答:∵定义在R上的奇函数f(x)是(-∞,0]上的增函数,且f(1)=2,f(-2)=-4,
可得f(-1)=-2,f(2)=4,
画出f(x)的图象:
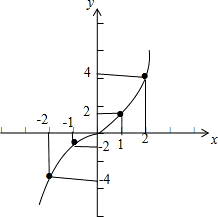
∵P={x|f(x+t)-4<0},Q={x|f(x)<-2},
解得P={x|x<2-t},Q={x|x<-1},
∵“x∈P”是“x∈Q”的充分不必要条件,
∴P⊆Q,
∴2-t<-1,解得t>3,
当t=3,可得P=Q,不满足“x∈P”是“x∈Q”的充分不必要条件,
∴t>3,
故选D;
点评:此题主要考查奇函数的定义及其应用,考查的知识点比较全面,利用了数形结合的方法,是一道中档题;
分析:根据定义在R上的奇函数f(x)是(-∞,0]上的增函数,且f(1)=2,f(-2)=-4,可以画出f(x)的图象,然后再求出P和Q集合,根据“x∈P”是“x∈Q”的充分不必要条件可得P⊆Q,从而求出t的范围;
解答:∵定义在R上的奇函数f(x)是(-∞,0]上的增函数,且f(1)=2,f(-2)=-4,
可得f(-1)=-2,f(2)=4,
画出f(x)的图象:
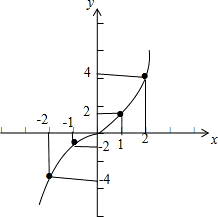
∵P={x|f(x+t)-4<0},Q={x|f(x)<-2},
解得P={x|x<2-t},Q={x|x<-1},
∵“x∈P”是“x∈Q”的充分不必要条件,
∴P⊆Q,
∴2-t<-1,解得t>3,
当t=3,可得P=Q,不满足“x∈P”是“x∈Q”的充分不必要条件,
∴t>3,
故选D;
点评:此题主要考查奇函数的定义及其应用,考查的知识点比较全面,利用了数形结合的方法,是一道中档题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)
 时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.
时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.