题目内容
点P是曲线f(x,y)=0上的动点,定点Q(1,1),
=-2
,则点M的轨迹方程是______.
| MP |
| MQ |
设点P(x0,y0),∵点P是曲线f(x,y)=0上的动点,∴f(x0,y0)=0.
设M(x,y),又Q(1,1),
=-2
,
∴(x0-x,y0-y)=-2(1-x,1-y),
即
,解得
,
代入f(x0,y0)=0得f(3x-2,3y-2)=0.
故点M的轨迹方程得f(3x-2,3y-2)=0.
故答案为f(3x-2,3y-2)=0.
设M(x,y),又Q(1,1),
| MP |
| MQ |
∴(x0-x,y0-y)=-2(1-x,1-y),
即
|
|
代入f(x0,y0)=0得f(3x-2,3y-2)=0.
故点M的轨迹方程得f(3x-2,3y-2)=0.
故答案为f(3x-2,3y-2)=0.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
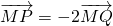 ,则点M的轨迹方程是________.
,则点M的轨迹方程是________.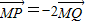 ,则点M的轨迹方程是 .
,则点M的轨迹方程是 .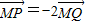 ,则点M的轨迹方程是 .
,则点M的轨迹方程是 .