Question

【题目】已知函数f（x）=2x+ax2+bcosx在点 处的切线方程为 ．
（Ⅰ）求a，b的值，并讨论f（x）在 上的增减性；
（Ⅱ）若f（x1）=f（x2），且0＜x1＜x2＜π，求证： ．
（参考公式： ）

Answer 1

【答案】解：（Ⅰ）由题意知f'（x）=2+2ax﹣bsinx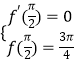，∴ 解得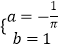
故 ， ．
当 时，f'（x）为减函数，且 ，
∴f'（x）＞0，f（x）为增函数．
（Ⅱ）证明：由f（x1）=f（x2），得 ，
所以 ，
两边同除以x1﹣x2 ， 得 ，
所以 ，
令 ，得 ，
得 ．
因为 ，
所以 ，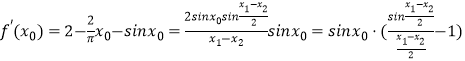
因为 ，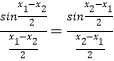
又 ，易知 ，所以 ，
又x0∈（0，π），所以sinx0＞0，故f'（x0）＜0，得 ．
【解析】（Ⅰ）求导数，利用函数f（x）=2x+ax2+bcosx在点 处的切线方程为 ，建立方程，求a，b的值，利用导数的正负讨论f（x）在 上的增减性；（Ⅱ）令 ，得 ，得 ，证明sinx0＞0，故f'（x0）＜0，即可得出结论．