题目内容
已知椭圆C: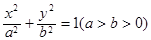 的离心率为
的离心率为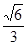 ,长轴长为
,长轴长为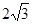 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线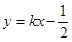 交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足
交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足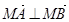 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.
【答案】
(I)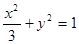 .(II)存在点
.(II)存在点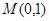 满足
满足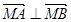 .
.
【解析】
试题分析:(I)利用椭圆的几何性质得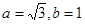 .
.
(II)通过研究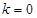 时,可知
时,可知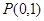 满足条件,若所求的定点M存在,则一定是P点.
满足条件,若所求的定点M存在,则一定是P点.
证明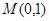 就是满足条件的定点.
就是满足条件的定点.
将直线方程与椭圆方程联立并整理,应用韦达定理,将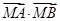 用坐标表示,根据
用坐标表示,根据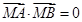
得到使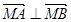 的点.
的点.
试题解析:(I)由题意得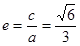 ,
,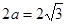 2分
2分
解得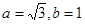 3分
3分
椭圆的方程为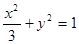 .
4分
.
4分
(II)当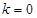 时,直线
时,直线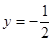 与椭圆交于两点的坐标分别为
与椭圆交于两点的坐标分别为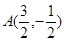 ,
,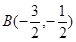
设y轴上一点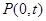 ,满足
,满足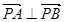 , 即
, 即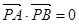 ,
,
∴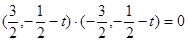 解得
解得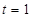 或
或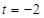 (舍),
(舍),
则可知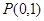 满足条件,若所求的定点M存在,则一定是P点. 6分
满足条件,若所求的定点M存在,则一定是P点. 6分
下面证明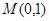 就是满足条件的定点.
就是满足条件的定点.
设直线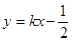 交椭圆于点
交椭圆于点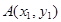 ,
,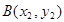 .
.
由题意联立方程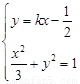
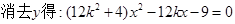 8分
8分
由韦达定理得,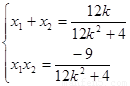 9分
9分
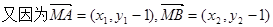
∴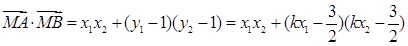
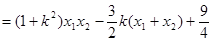
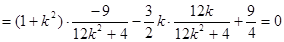 11分
11分
∴ 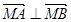 ,即在y轴正半轴上存在定点
,即在y轴正半轴上存在定点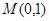 满足条件. 12分
满足条件. 12分
解法2:
设y轴上一点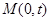 ,满足
,满足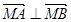 , 即,
, 即,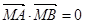 5分
5分
设直线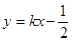 交椭圆于点
交椭圆于点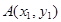 ,
, 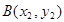 .
.
由题意联立方程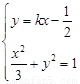
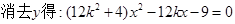 7分
7分
由韦达定理得,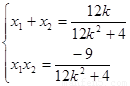 8分
8分
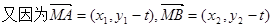
∴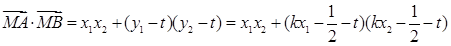
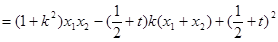
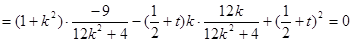 10分
10分
整理得,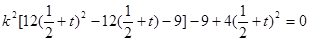
由对任意k都成立,得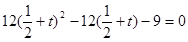
且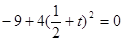
解得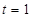 11分
11分
所以存在点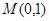 满足
满足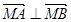 .
12分
.
12分
考点:椭圆的几何性质,直线与椭圆的位置关系,平面向量的坐标运算.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为