题目内容
已知抛物线y2=2px(p＞0)，过焦点F的弦的倾斜角为θ(θ≠0),且与抛物线相交于A、B两点.(1)求证：|AB|=
;
(2)求|AB|的最小值.
（1）证明：如图，焦点F的坐标为F（
,0）.
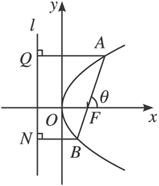
设过焦点、倾斜角为θ的直线方程为y=tanθ·（x-
）,与抛物线方程联立，消去y并整理，得
tan2θ·x2-(2p+ptan2θ)x+
=0.
此方程的两根应为交点A、B的横坐标，根据韦达定理，有x1+x2=
.
设A、B到抛物线的准线x=-
的距离分别为|AQ|和|BN|，根据抛物线的定义，有|AB|=|AF|+|FB|=|AQ|+|BN|=x1+x2+p=
.
（2）解析：因|AB|=
的定义域是0＜θ＜π，又sin2θ≤1，
所以，当θ=
时，|AB|有最小值2p.
练习册系列答案
相关题目