Question

如图，在长方体ABCD—A₁B₁C₁D₁中，AB=6,AD=4,AA₁=3，分别过BC、A₁D₁的两个平行截面将长方体分成三部分，其体积分别记为V₁=V_aEA₁—DFD₁，V₂=V_{EBE1A1—FCF1D1},V₃=V_{B1E1B—C1F1C}.若V₁∶V₂∶V₃=1∶4∶1，则截面A₁EFD₁的面积为(　　)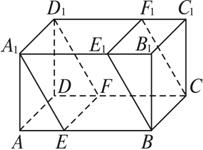

 

A.410                  B.83                      C.413                    D.16

Answer 1

思路解析：可以看出、所分的三个部分分别是三棱柱、四棱柱、三棱柱、由V₁∶V₂∶V₃=1∶4∶1、可得S_△AA1E∶S_{四边形EBE1A1}∶S_△BB1E1=1∶4∶1,显然矩形ABB₁A₁的面积为18,

所以S_△AEA1=3,进一步求得AE=2.则由勾股定理求得A₁E=,所以截面A₁EFD₁的面积为4.故选C.

答案：C