题目内容
.(本小题满分14分)已知椭圆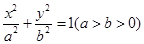 的一个焦点
的一个焦点 与抛物线
与抛物线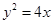 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为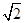 ,倾斜角为
,倾斜角为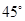 的直线
的直线 过点
过点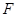 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为 ,试求抛物线
,试求抛物线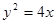 上一点
上一点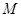 ,使得
,使得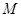 与
与 关于直线
关于直线 对称,求出点
对称,求出点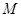 的坐标.
的坐标.
【答案】
(1)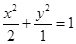 ;
;
(2)抛物线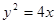 上存在一点
上存在一点 ,使得
,使得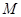 与
与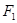 关于直线
关于直线 对称.
对称.
【解析】(I)根据抛物线的方程可以求出椭圆的焦点坐标,进而求出c值.
再利用抛物线准线被椭圆截得的弦长为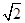 ,可得交点坐标为
,可得交点坐标为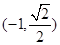 ,
,
然后代入椭圆方程再结合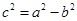 ,解方程组即可.
,解方程组即可.
(2)易求出直线l的方程,然后求出焦点F(-1,0)关于直线l的对称点,根据对称点在抛物线上.确定抛物线的方程.
解:(1)抛物线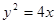 的焦点为
的焦点为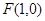 ,准线方程为
,准线方程为 ,……………2分
,……………2分
∴  ① …………………3分
① …………………3分
又椭圆截抛物线的准线 所得弦长为
所得弦长为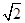 , ∴ 得上交点为
, ∴ 得上交点为 ,
,
∴ 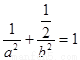 ②…………………4分
②…………………4分
由①代入②得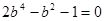 ,解得
,解得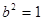 或
或 (舍去),
(舍去),
从而 …………………6分
…………………6分
∴ 该椭圆的方程为该椭圆的方程为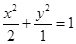 …………………7分
…………………7分
(2)∵
倾斜角为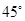 的直线
的直线 过点
过点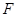 ,
,
∴ 直线 的方程为
的方程为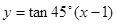 ,即
,即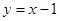 ,…………………8分
,…………………8分
由(1)知椭圆的另一个焦点为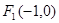 ,设
,设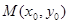 与
与 关于直线
关于直线 对称,…9分
对称,…9分
则得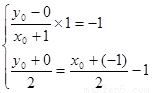 ……10分 解得
……10分 解得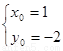 ,即
,即
又 满足
满足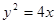 ,故点
,故点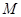 在抛物线上. …………………12分
在抛物线上. …………………12分
所以抛物线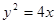 上存在一点
上存在一点 ,使得
,使得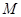 与
与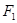 关于直线
关于直线 对称.……13分
对称.……13分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)