题目内容
如图,已知直四棱柱ABCD—A1B1C1D1,其高为m,底面是边长为2的菱形,且∠ABC=120°.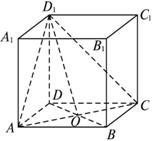
(1)求证:平面D1AC⊥平面BDD1B1;
(2)若直线AD1与平面BDD1B1所成的角为30°,求二面角D1-AC-D的大小;
(3)若异面直线BC1与CD1所成角的余弦值为![]() ,求m的大小.
,求m的大小.
(1)证明:由直四棱柱知DD1⊥平面ABCD,
又AC![]() 平面ABCD,∴AC⊥DD1.
平面ABCD,∴AC⊥DD1.
又四边形ABCD为菱形,∴AC⊥BD.
而DD1∩BD=D,∴AC⊥平面BDD1B1.
又AC![]() 平面D1AC,∴平面D1AC⊥平面BDD1B1.
平面D1AC,∴平面D1AC⊥平面BDD1B1.
(2)解:如图,连结D1O,

∵AC⊥平面BDD1B1,且直线AD1与平面BDD1B1所成角为30°,
∴∠AD1O=30°,且AC⊥DO,AC⊥D1O.
∴∠D1OD为二面角D1ACD的平面角.
又∵△ABD为正三角形,且AB=2,
∴AO=![]() ,D1O=AOcot30°=3.
,D1O=AOcot30°=3.
∴cos∠D1OD=![]() =
=![]() ,
,
即所求二面角的平面角为arccos![]() .
.
注:若求出m=2![]() ,则有所求二面角的平面角为arcsin
,则有所求二面角的平面角为arcsin![]() 或arctan2
或arctan2![]() .
.
(3)解:∵AD1∥BC1,
∴∠AD1C为异面直线BC1与CD1所成角或其补角.
∴cos∠AD1C=±![]() .
.
在△AD1C中,由余弦定理得AC2=![]() -2AD1·CD1cos∠AD1C,
-2AD1·CD1cos∠AD1C,
即12=2(m2+4)±2(m2+4)×![]() .
.
解得m=![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案 如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.
如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.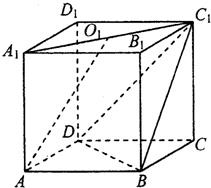 如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点.
如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点. 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: