题目内容
已知f(x)对一切实数x,y都有f(x+y)=f(x)+f(y),f(1)=2,当x>0时,f(x)<0.
(1)证明f(x)为奇函数;
(2)用定义证明f(x)为R上的减函数;
(3)解不等式f(x-1)-f(1-2x-x2)<4
答案:
解析:
解析:
|
(1)证明,依题意取 由x的任意性可知f(x)为奇函数 4分 (2)证明: (3)解:依题意有 所以不等式的解集为 |

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
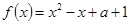
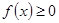 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。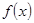 在区间
在区间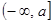 上的最小值
上的最小值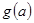 的表达式。
的表达式。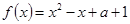
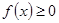 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。 在区间
在区间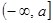 上的最小值
上的最小值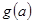 的表达式。
的表达式。