题目内容
【题目】如图,四边形![]() 和四边形
和四边形![]() 均是直角梯形,
均是直角梯形,![]() ,二面角
,二面角![]() 是直二面角,
是直二面角,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() 面
面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2)![]()
【解析】分析:(1)利用线面、面面平行的判定和性质定理即可证明;
(2)根据条件,建立相应的空间直角坐标系,利用平面的法向量所成角的余弦值来得到对应的二面角的余弦值的大小.
详解:(Ⅰ)由已知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
同理可得:![]() 平面
平面![]() .
.
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(Ⅱ)因为二面角![]() 是直二面角,
是直二面角,
所以平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
又![]() ,有
,有![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ;
;
由已知得,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则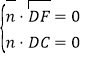 ,即
,即![]() .
.
不妨取![]() ,则
,则![]() ,
,
取面![]() 的一个法向量
的一个法向量![]() ,
,
所以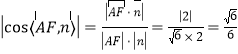 .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中,能较好地反映计算机在第![]() 天被感染的数量
天被感染的数量![]() 与
与![]() 之间的关系的是
之间的关系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()