Question

已知关于x的不等式ax²+bx+c＜0的解集是{x|x＜-2或x＞-}，求不等式ax²-bx+c＞0的解集.

   

Answer 1

思路分析：由题意可知，-2、是方程ax²+bx+c=0的两根，由韦达定理可得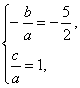注意观察要求不等式与已知条件之间的联系.

    解：由条件知，-2、-是方程ax²+bx+c=0的两根，且a＜0.

    ∴-2-=-，(-2)×(-)=.

    ∴b=a，c=a.

    从而不等式ax²-bx+c＞0变为a(x²-x+1)＞0.

    ∵a＜0，

    ∴2x²-5x+2＜0，

    即(x-2)(2x-1)＜0.解得＜x＜2.

    ∴不等式的解集为{x|＜x＜2}.