题目内容
【题目】如图,椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点、上顶点分别为点
,右顶点、上顶点分别为点![]() ,
,
已知椭圆![]() 的焦距为
的焦距为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当
两点,当![]() 面积取得最大时,求直线
面积取得最大时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题(1)由椭圆![]() 的焦距为
的焦距为![]() 可得
可得![]() ,再由两点的距离公式,结合
,再由两点的距离公式,结合![]() 的关系,解得
的关系,解得![]() ,进而得到椭圆方程;(2)设直线
,进而得到椭圆方程;(2)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,运用韦达定理和判别式大于零,以及弦长公式,点到直线的距离公式和三角形的面积公式,结合基本不等式成立的条件即可得到直线方程.
,代入椭圆方程,运用韦达定理和判别式大于零,以及弦长公式,点到直线的距离公式和三角形的面积公式,结合基本不等式成立的条件即可得到直线方程.
试题解析:(1)椭圆![]() 的焦距为
的焦距为![]() ,所以
,所以![]() ,
, ![]()
由已知![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,
,
椭圆方程为![]()
(2)解:由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]()
由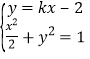 ,消去
,消去![]() 得关于
得关于![]() 的方程:
的方程:![]()
由直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,
两点,![]() 解得
解得![]()
又由韦达定理得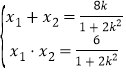
![]()
![]()
原点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() .
.
令![]() ,则
,则![]()
![]()
当且仅当![]() 即
即![]() 时,
时,![]()
此时![]() .
.
所以,所求直线方程为![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和三角形面积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】随着苹果6手机的上市,很多消费者觉得价格偏高,尤其是一部分大学生可望而不可及,因此“国美在线”推出无抵押分期付款购买方式,某分期店对最近100位采用分期付款的购买者进行统计,统计结果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频 数 | 35 | 25 | a | 10 | b |
已知分3期付款的频率为0.15,并且店销售一部苹果6,顾客分1期付款,其利润为1千元;分2期或3期付款,其利润为1.5千元;分4期或5期付款,其利润为2千元,以频率作为概率.
(1)求事件A:“购买的3位顾客中,至多有1位分4期付款”的概率;
(2)用X表示销售一该手机的利润,求X的分布列及数学期望E(x)