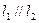题目内容
若直线 :
: 平行于直线
平行于直线 ,则直线
,则直线 在两轴截距之和为
在两轴截距之和为
 :
: 平行于直线
平行于直线 ,则直线
,则直线 在两轴截距之和为
在两轴截距之和为| A. 6 | B. 2 | C. -1 | D. -2 |
B
根据两个直线平行斜率相等,求出a的值,再令x=0和y=0,求出它在坐标轴上截距,即求它在坐标轴上截距的和.
解:∵直线l:x+ay+2=0平行于直线2x-y+3=0,
∴2=- ,解得a=-
,解得a=- ,代入直线l:x+ay+2=0,得2x-y+4=0,
,代入直线l:x+ay+2=0,得2x-y+4=0,
对于方程2x-y+4=0分别令x=0和y=0,求出它在坐标轴上截距为:4,-2;
故它在坐标轴上截距的和是2.
故选B.
解:∵直线l:x+ay+2=0平行于直线2x-y+3=0,
∴2=-
 ,解得a=-
,解得a=- ,代入直线l:x+ay+2=0,得2x-y+4=0,
,代入直线l:x+ay+2=0,得2x-y+4=0,对于方程2x-y+4=0分别令x=0和y=0,求出它在坐标轴上截距为:4,-2;
故它在坐标轴上截距的和是2.
故选B.

练习册系列答案
相关题目
 且在两坐标轴上的截距相等,则这直线方程为( )
且在两坐标轴上的截距相等,则这直线方程为( )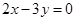
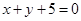
 的直线与直线
的直线与直线 平行,则实数
平行,则实数 的值为( )
的值为( )







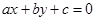 的倾斜角为
的倾斜角为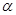 ,且
,且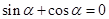 ,则
,则 满足( )
满足( )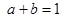 B
B 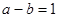 C
C 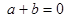 D
D 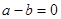
 ,
, ,
, ,则△
,则△ 边上的中线所在的直线方程是__
边上的中线所在的直线方程是__ ___________
___________
 ___
___ 直线l被两平行线l1:x+y-5=0
直线l被两平行线l1:x+y-5=0 和直线l2:x+y-3=0所截得的线段长为2,且直线l过
和直线l2:x+y-3=0所截得的线段长为2,且直线l过 (5,2)点,求直线l的方程。
(5,2)点,求直线l的方程。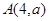 和
和 的直线与直线
的直线与直线 平行,则
平行,则 的值( )
的值( ) 
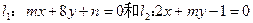 ,试确定
,试确定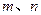 的值,使得:
的值,使得: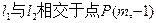 ; (2)
; (2)