题目内容
设u，v∈R，且|u|≤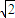
，v＞0，则（u-v）2+（
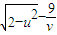）2的最小值为（ ）A．4
B．2
C．8
D．
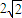
【答案】分析：设P（u，
），Q（v，
），则（u-v）2+（
）2的看成是P，Q两点的距离的平方，P点在圆x2+y2=2上，Q点在双曲线y=
，如图，由图象得出P，Q两点的最小距离即可．
解答：
解：设P（u，
），Q（v，
），
则（u-v）2+（
）2的看成是P，Q两点的距离的平方，
P点在圆x2+y2=2上，Q点在双曲线y=
，如图，
由图象得出P，Q两点的最小距离为AB=2
则（u-v）2+（
）2的最小值为8，
故选C．
点评：此题考查学生灵活运用重要不等式求函数的最值，灵活运用两点间的距离公式化简求值，是一道中档题．
），Q（v，），则（u-v）2+（）2的看成是P，Q两点的距离的平方，P点在圆x2+y2=2上，Q点在双曲线y=，如图，由图象得出P，Q两点的最小距离即可．解答：
解：设P（u，），Q（v，），则（u-v）2+（
）2的看成是P，Q两点的距离的平方，P点在圆x2+y2=2上，Q点在双曲线y=
，如图，由图象得出P，Q两点的最小距离为AB=2
则（u-v）2+（
）2的最小值为8，故选C．
点评：此题考查学生灵活运用重要不等式求函数的最值，灵活运用两点间的距离公式化简求值，是一道中档题．
练习册系列答案
相关题目
设u，v∈R，且|u|≤
，v＞0，则（u-v）2+（
-
）2的最小值为（ ）
| 2 |
| 2-u2 |
| 9 |
| v |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、2
|
,v＞0,则(u－v)2+(
)2的最小值为( )
，v＞0，则（u-v）2+（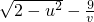
）2的最小值为