题目内容
已知三棱柱ABC-A1B1C1的侧棱与底面垂直，体积为
，底面是边长为
的正三角形，若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为( )
A． | B． | C． | D． |
B
解析试题分析：设点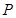
在平面
内的投影是点
，连接
，
，
即是所求，如图：
底面积为
，所以三棱柱的高是
，则
，点是
的中心，分的高为
，所以
，则
，故
.
考点：1.三棱柱的体积；2.直线与平面所成的角
练习册系列答案
相关题目
如图所示是一个几何体的三视图，若该几何体的体积为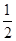
，则主视图中三角形的高x的值为（ ）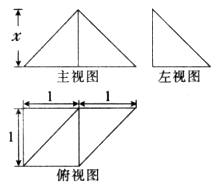
| A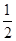． | B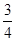． | C．1 | D． |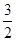
将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体包括（ ）
| A．一个圆台、两个圆锥 | B．一个圆柱、两个圆锥 |
| C．两个圆台、一个圆柱 | D．两个圆柱、一个圆台 |
右图是某几何体的三视图，则该几何体的表面积等于( )
A． | B． |
C． | D． |
一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（ ）
A．外接球的半径为 | B．体积为 |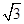
C．表面积为 | D．外接球的表面积为 |
的正方形，剪去阴影部分后，得到圆锥的侧面和底面的展开图，则圆锥的体积是（ ）.
圆
绕直线
旋转一周所得的几何体的体积为（ ）
A． | B． | C． | D． |