Question

设a=x²-x+1，b=x²-2x，c=2x-1，若a，b，c分别为△ABC的相应三边长，
（1）求实数x的取值范围；
（2）求△ABC的最大内角；
（3）设△ABC的外接圆半径为R，内切圆半径为r，求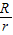的取值范围．

Answer 1

【答案】分析：（1）构成三角形的条件是三边均为正数，且任意两边之和大于第三边，可求实数x的取值范围；
（2）先根据边长之间的关系，确定A为最大角，进而利用余弦定理，可求△ABC的最大内角；
（3）根据正弦定理确定△ABC的外接圆半径为R，根据等面积确定内切圆半径为r，从而可得的不等式，进而可求其取值范围．
解答：解：（1）由题意，
∵构成三角形的条件是三边均为正数，∴，∴x＞2，
又∵任意两边之和大于第三边
∴a-b=x+1＞0，a-c=（x-1）（x-2）＞0
∴b+c＞a，∴x²-2x+2x-1＞x²-x+1，∴x＞2…（4分）
（2）由（1）可知A为最大角，，
∵A为三角形的内角，∴A=120°．…（10分）
（3）根据正弦定理得：…（11分）
利用三角形的面积相等可得，
∴…（12分）
∴…（14分）
令x-2=t＞0，则
∵t＞0，
∴
∴
∴…（16分）
点评：本题的考点是解三角形，主要考查构成三角形的条件，考查正弦、余弦定理，同时考查基本不等式的运用，其中构建的表达式是解题的关键．