题目内容
在△ABC中角A、B、C的对边分别为a、b、c,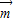 =(a,cosB),
=(a,cosB),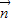 =(b,cosA)且
=(b,cosA)且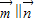 ,
,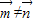 ,
,(1)判断△ABC的形状;
(2)求sinA+sinB的取值范围;
(3)若abx=ac+bc,x∈R+试确定log2x的取值范围.
【答案】分析:(1)由两个向量共线的性质可得acosA=bcosB,再由正弦定理求得sin2A=sin2B,又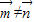 ,故2A+2B=π,即 A+B=
,故2A+2B=π,即 A+B=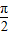 ,则 C=
,则 C=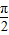 ,由此可得△ABC的形状.
,由此可得△ABC的形状.
(2)由于 sinA+sinB=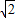 sin(A+
sin(A+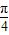 ),0<A<
),0<A<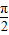 ,可得
,可得 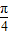 <A+
<A+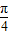 <
<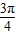 ,从而求得
,从而求得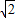 sin(A+
sin(A+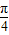 )的范围.
)的范围.
(3)由abx=ac+bc,得x=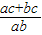 ,再由正弦定理可得 x=
,再由正弦定理可得 x=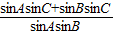 =
=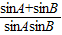 ,设 sinA+sinB=t∈(1,
,设 sinA+sinB=t∈(1,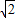 ],可得 x=
],可得 x=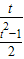 =
=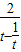 ,利用基本不等式求得x的范围,即可求得log2x的取值范围.
,利用基本不等式求得x的范围,即可求得log2x的取值范围.
解答:解:(1)∵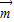 =(a,cosB),
=(a,cosB),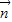 =(b,cosA),且
=(b,cosA),且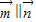 ,∴acosA=bcosB.-----(1分)
,∴acosA=bcosB.-----(1分)
由正弦定理,得sinAcosA=sinBcosB,即sin2A=sin2B.-----(2分)
又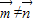 ,所以,2A+2B=π,即 A+B=
,所以,2A+2B=π,即 A+B=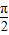 ,则 C=
,则 C=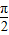 ,--------(3分)
,--------(3分)
∴△ABC是直角三角形.---------(4分)
(2)sinA+sinB=sinA+sin(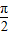 -A)=sinA+cosA=
-A)=sinA+cosA=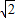 sin(A+
sin(A+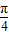 ).---(6分)
).---(6分)
∵0<A<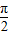 ,∴
,∴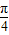 <A+
<A+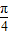 <
<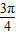 ,∴
,∴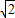 ×
×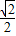 <
<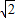 sin(A+
sin(A+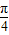 )≤
)≤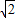 ,故sinA+sinB的取值范围是(1,
,故sinA+sinB的取值范围是(1,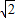 ].-------------(8分)
].-------------(8分)
(3)若abx=ac+bc,x∈R+,则 x=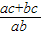 ,
,
由正弦定理,得 x=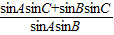 =
=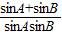 ,---------(9分)
,---------(9分)
设 sinA+sinB=t∈(1,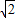 ],则 t2=1+2sinAcosA,所以sinAcosA=
],则 t2=1+2sinAcosA,所以sinAcosA=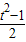 ,----(10分)
,----(10分)
即 x=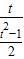 =
=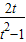 =
=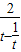 ≥
≥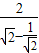 =2
=2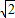 ,∴log2x≥
,∴log2x≥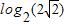 =
=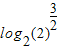 =
= ,
,
所以log2x的取值范围为[ ,+∞).-----------(12分)
,+∞).-----------(12分)
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,正弦定理、两角和差的正弦公式,正弦函数的定义域和值域,基本不等式的应用,属于中档题.
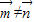 ,故2A+2B=π,即 A+B=
,故2A+2B=π,即 A+B=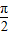 ,则 C=
,则 C=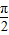 ,由此可得△ABC的形状.
,由此可得△ABC的形状.(2)由于 sinA+sinB=
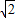 sin(A+
sin(A+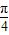 ),0<A<
),0<A<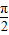 ,可得
,可得 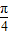 <A+
<A+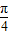 <
<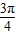 ,从而求得
,从而求得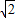 sin(A+
sin(A+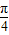 )的范围.
)的范围.(3)由abx=ac+bc,得x=
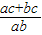 ,再由正弦定理可得 x=
,再由正弦定理可得 x=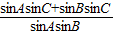 =
=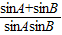 ,设 sinA+sinB=t∈(1,
,设 sinA+sinB=t∈(1,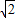 ],可得 x=
],可得 x=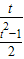 =
=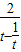 ,利用基本不等式求得x的范围,即可求得log2x的取值范围.
,利用基本不等式求得x的范围,即可求得log2x的取值范围.解答:解:(1)∵
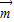 =(a,cosB),
=(a,cosB),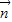 =(b,cosA),且
=(b,cosA),且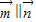 ,∴acosA=bcosB.-----(1分)
,∴acosA=bcosB.-----(1分)由正弦定理,得sinAcosA=sinBcosB,即sin2A=sin2B.-----(2分)
又
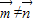 ,所以,2A+2B=π,即 A+B=
,所以,2A+2B=π,即 A+B=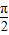 ,则 C=
,则 C=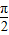 ,--------(3分)
,--------(3分)∴△ABC是直角三角形.---------(4分)
(2)sinA+sinB=sinA+sin(
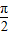 -A)=sinA+cosA=
-A)=sinA+cosA=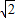 sin(A+
sin(A+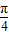 ).---(6分)
).---(6分)∵0<A<
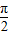 ,∴
,∴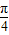 <A+
<A+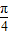 <
<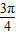 ,∴
,∴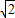 ×
×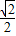 <
<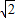 sin(A+
sin(A+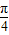 )≤
)≤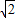 ,故sinA+sinB的取值范围是(1,
,故sinA+sinB的取值范围是(1,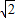 ].-------------(8分)
].-------------(8分)(3)若abx=ac+bc,x∈R+,则 x=
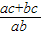 ,
,由正弦定理,得 x=
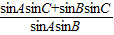 =
=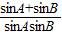 ,---------(9分)
,---------(9分)设 sinA+sinB=t∈(1,
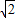 ],则 t2=1+2sinAcosA,所以sinAcosA=
],则 t2=1+2sinAcosA,所以sinAcosA=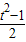 ,----(10分)
,----(10分)即 x=
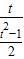 =
=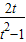 =
=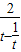 ≥
≥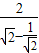 =2
=2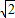 ,∴log2x≥
,∴log2x≥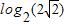 =
=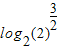 =
= ,
,所以log2x的取值范围为[
 ,+∞).-----------(12分)
,+∞).-----------(12分)点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,正弦定理、两角和差的正弦公式,正弦函数的定义域和值域,基本不等式的应用,属于中档题.

练习册系列答案
相关题目