Question

已知三棱锥S-ABC的棱长均相等，E是SA的中点，F为△ABC的中心，则异面直线EF与AB所成的角为

 

．

Answer 1

分析：如图，作CD⊥AB于D，分别以DB、DC为x、y轴，D为原点，建立如图所求空间直角坐标系．设三棱锥S-ABC的棱长为2，求出向量

DA

，

FE

的坐标，利用空间向量的夹角公式加以计算，可得异面直线EF与AB所成的角．

解答：解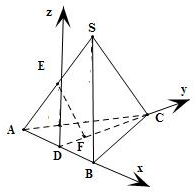：设三棱锥S-ABC的棱长都等于2，
在平面ABC内作CD⊥AB于D，则点F在CD上且满足CF=2DF，
分别以DB、DC为x、y轴，D为原点，建立如图所求空间直角坐标系
可得D（0，0，0），A（-1，0，0），F（0，

3

3

，0），
S（0，

3

3

，

2 6

3

）可得SA的中点是E（-

1

2

，

3

6

，

6

3

）
∴

DA

=(-1，0，0)，

FE

=(-

1

2

，-

3

6

，

6

3

)
可得cos＜

DA

，

FE

＞=

-1×(- 1 2 )+0×(- 3 6 )+0× 6 3

1× 1 4 + 1 12 + 2 3

=

1

2

，
∴＜

DA

，

FE

＞=60°，可得异面直线EF与AB所成的角60°．
故答案为：60°

点评：本题在正四面体中求异面直线所成角的大小，着重考查了正四面体的性质、利用空间向量求异面直线所成角的大小等知识，属于中档题．