题目内容
a、b是不等于1的正数，θ∈（
，2π），若atanθ＞btanθ＞1，则下列不等式成立的是
- A.a＞b＞1
- B.a＜b＜1
- C.b＜a＜1
- D.b＞a＞1
B
分析：由已知可得，tanθ＜0，结合已知atanθ＞btanθ＞1，及a0=b0=1可判断a，b的大小
解答：∵θ∈（，2π）
∴tanθ＜0
∵a＞0，b＞0且a≠1，b≠1且atanθ＞btanθ＞1，
而a0=b0=1
∴atanθ＞a0，btanθ＞b0，
∴0＜a＜b＜1
故选B
点评：本题主要考查了指数函数的单调性的应用，属于基础试题
分析：由已知可得，tanθ＜0，结合已知atanθ＞btanθ＞1，及a0=b0=1可判断a，b的大小
解答：∵θ∈（
，2π）∴tanθ＜0
∵a＞0，b＞0且a≠1，b≠1且atanθ＞btanθ＞1，
而a0=b0=1
∴atanθ＞a0，btanθ＞b0，
∴0＜a＜b＜1
故选B
点评：本题主要考查了指数函数的单调性的应用，属于基础试题
练习册系列答案
相关题目
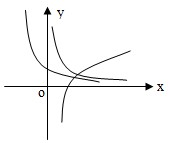
如图是函数f（x）=ax、g（x）=xb、h（x）=logcx（a、c是不等于1的正实数），则a、b、c的大小关系是（ ）
如图是函数f（x）=ax、g（x）=xb、h（x）=logcx（a、c是不等于1的正实数），则a、b、c的大小关系是
、
、
（a、c是不等于1的正实数），则a、b、c的大小关系是（ ）