题目内容
已知函数![]() .
.
(1)求![]() 在[0,1]上的极值;
在[0,1]上的极值;
(2)若对任意![]() ∈[
∈[![]() ],不等式
],不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在[0,1]上恰有两个不同的实根,求实数
在[0,1]上恰有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
解:(1)![]() ,
,
令![]() 得
得![]() 或
或![]() (舍去);
(舍去);
当0≤![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() ≤1时,
≤1时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() 为函数
为函数![]() 在[0,1]上的极大值.
在[0,1]上的极大值.
(2)由![]() 得
得
![]() ①
①
设![]() ,
,
![]() ,
,
依题意知![]() 或
或![]() 在[
在[![]() ]上恒成立.
]上恒成立.
∵![]() ,
,
∴![]() 与
与![]() 都在[
都在[![]() ]上单调,要使不等式①成立,
]上单调,要使不等式①成立,
当且仅当![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
(3)由![]() 得
得
![]() ,
,
令![]() ,
,
则![]() ,
,
当 时,
时,![]() ,于是
,于是![]() 在
在 上递增;
上递增;
当 时,
时,![]() ,于是
,于是![]() 在
在 上递减.
上递减.
而 ,所以
,所以![]() 在[0,1]上恰有两个不同的实根等价于:
在[0,1]上恰有两个不同的实根等价于:
所以![]() .
.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. ,
,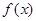 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. ,
,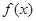 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.