题目内容
设f(x)=lg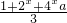 ,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围.
,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围.
解:当x∈(-∞,1]时f(x)=lg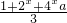 有意义的函数问题,
有意义的函数问题,
转化为1+2x+4xa>0在x∈(-∞,1]上恒成立的不等式问题.
不等式1+2x+4xa>0在x∈(-∞,1]上恒成立,
即:a>-[( )2x+(
)2x+( )x]在x∈(-∞,1]上恒成立.
)x]在x∈(-∞,1]上恒成立.
设t=( )x,则t≥
)x,则t≥ ,又设g(t)=t2+t,其对称轴为t=-
,又设g(t)=t2+t,其对称轴为t=-
∴g(t)=t2+t在[ ,+∞)上为增函数,当t=
,+∞)上为增函数,当t= 时,g(t)有最小值g(
时,g(t)有最小值g( )=(
)=( )2+
)2+ =
=
所以a的取值范围是a>- .
.
分析:f(x)有意义,则真数大于0,所以问题转化为1+2x+4xa>0在x∈(-∞,1]上恒成立的不等式问题.分离参数,转化为求函数的最值解决.注意到4x=(2x)2,换元法转化为求二次函数在特定区间上的最值问题.
点评:本题考查对数函数的定义域、不等式恒成立问题,考查换元法和转化思想.
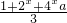 有意义的函数问题,
有意义的函数问题,转化为1+2x+4xa>0在x∈(-∞,1]上恒成立的不等式问题.
不等式1+2x+4xa>0在x∈(-∞,1]上恒成立,
即:a>-[(
 )2x+(
)2x+( )x]在x∈(-∞,1]上恒成立.
)x]在x∈(-∞,1]上恒成立.设t=(
 )x,则t≥
)x,则t≥ ,又设g(t)=t2+t,其对称轴为t=-
,又设g(t)=t2+t,其对称轴为t=-
∴g(t)=t2+t在[
 ,+∞)上为增函数,当t=
,+∞)上为增函数,当t= 时,g(t)有最小值g(
时,g(t)有最小值g( )=(
)=( )2+
)2+ =
=
所以a的取值范围是a>-
 .
.分析:f(x)有意义,则真数大于0,所以问题转化为1+2x+4xa>0在x∈(-∞,1]上恒成立的不等式问题.分离参数,转化为求函数的最值解决.注意到4x=(2x)2,换元法转化为求二次函数在特定区间上的最值问题.
点评:本题考查对数函数的定义域、不等式恒成立问题,考查换元法和转化思想.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
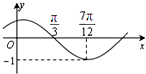 已知函数f(x)=Asin(ωx+φ)(其中
已知函数f(x)=Asin(ωx+φ)(其中