题目内容
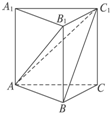
长方体ABCD-A1B1C1D1,AB=2,AD=2,AA1=
,则点D到平面ACD1的距离是( )
| 6 |
A.
| B.
| C.
| D.2 |
以D为原点,以DA为x轴,以DC为y轴,以DD1为z轴,
建立空间直角坐标系,
∵长方体ABCD-A1B1C1D1,AB=2,AD=2,AA1=
,
∴A(2,0,0),C(0,2,0),D1(0,0,
),D(0,0,0),
∴
=(-2,0,
),
=(-2,2,0),
=(-2,0,0),
设平面ACD1的法向量
=(x,y,z),
则
,取x=1,得
=(1,1,
),
∴点D到平面ACD1的距离是d=
=
=
.
故选:C.

建立空间直角坐标系,
∵长方体ABCD-A1B1C1D1,AB=2,AD=2,AA1=
| 6 |
∴A(2,0,0),C(0,2,0),D1(0,0,
| 6 |
∴
| AD1 |
| 6 |
| AC |
| AD |
设平面ACD1的法向量
| n |
则
|
| n |
| ||
| 3 |
∴点D到平面ACD1的距离是d=
|
| ||||
|
|
| |-2| | ||||
|
| ||
| 2 |
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
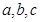 为直线,
为直线,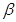 为平面,给出下列命题
为平面,给出下列命题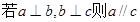 ②
②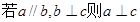
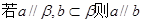 ④
④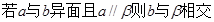
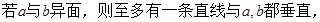 其中真命题的个数是( )
其中真命题的个数是( )