Question

将圆x²+y²-2x+4y=0按向量a=(-1，2)平移后得到⊙O，直线l与⊙O相交于A，B两点，若在⊙O上存在点C，使=a，求直线l的方程及对应的点C的坐标．

Answer 1

答案：解：圆x²+y²-2x+4y=0按a(-1，2)平移后得⊙O的方程为x²+y²=5

由=λa=(-λ，2λ)且C在⊙O上

∴λ=±1 

当λ=1时，C的坐标为(-1，2)，设A(x₁，y₁)，

B(x₂，y₂)  则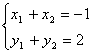

直线l的方程为y=kx+b

联立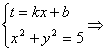(1+k²)x²+2kbx+b²-5=0

∴

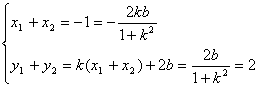
解得k=  b=

∴直线l的方程为y= 

当λ=-1时，C点坐标为(1，-2)，由对称性知l

的方程为：y=