题目内容
已知数列{![]() }、{
}、{![]() }满足:
}满足:![]() 。
。
(Ⅰ)求![]() ;
;
(Ⅱ)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() ,不等式
,不等式![]() 恒成立时,求实数
恒成立时,求实数![]() 的取值范围。
的取值范围。
(Ⅰ)![]()
(Ⅱ)![]()
(Ⅲ)![]()
解析:
(Ⅰ) ![]()
∵![]() ∴
∴![]() ……4分
……4分
(Ⅱ)∵![]() ∴
∴![]() ……5分
……5分
∴数列{![]() }是以-4为首项,-1为公差的等差数列.
}是以-4为首项,-1为公差的等差数列.
∴![]() . ……7分
. ……7分
(Ⅲ)由于![]() ,所以
,所以![]() ,从而
,从而![]() ..……8分
..……8分
∴![]()
∴![]() ……10分
……10分
由条件可知![]() 恒成立即可满足条件,设
恒成立即可满足条件,设
![]()
当![]() 时,
时,![]() 恒成立
恒成立
当![]() 时,由二次函数的性质知不可能成立
时,由二次函数的性质知不可能成立
当![]() 时,对称轴
时,对称轴 ![]() ,
,
![]() 在
在![]() 为单调递减函数.
为单调递减函数.
![]() ,
,
∴![]() ∴
∴![]() 时
时![]() 恒成立
恒成立
综上知:![]() 时,
时,![]() 恒成立……14分
恒成立……14分

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 的反函数为
的反函数为
 为等差数列,
为等差数列, 为其前
为其前 项和
项和
 的反函数为
的反函数为 ,则
,则 。
。 平面ABC,AB
平面ABC,AB BC,DA=AB=BC=
BC,DA=AB=BC= ,则球O的体积等于 。
,则球O的体积等于 。 (
( ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。
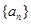 为等差数列,
为等差数列,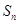 为其前
为其前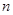 项和
项和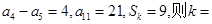
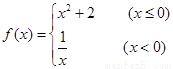 的反函数为
的反函数为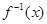 ,则
,则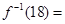 。
。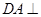 平面ABC,AB
平面ABC,AB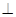 BC,DA=AB=BC=
BC,DA=AB=BC=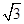 ,则球O的体积等于 。
,则球O的体积等于 。 (
(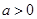 ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的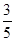 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。