题目内容
从曲线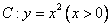 上一点
上一点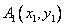 引曲线C的第一条切线
引曲线C的第一条切线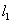 ,
,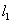 交
交 轴于点
轴于点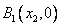 ,过点
,过点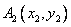 引曲线C的第二条切线
引曲线C的第二条切线 ,
, 交
交 轴于点
轴于点 ,…如此反复作下去,由切线
,…如此反复作下去,由切线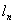 得到点列
得到点列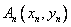 ,
,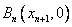 ,
,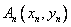 的横坐标组成数列
的横坐标组成数列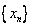 ,
,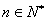
(1)若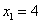 ,求数列
,求数列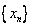 的通项公式;
的通项公式;
(2)若对于任意的正整数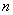 都有
都有 恒成立,且
恒成立,且 ,求
,求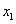 的最大值;
的最大值;
(3)在(1)的条件下,记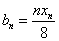 ,数列
,数列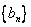 的前
的前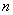 项和为
项和为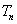 ,试比较
,试比较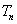 与1的大小。
与1的大小。
【答案】
解:(1) 1分
1分  的方程为
的方程为 且
且
令 得
得 即
即
又Bn(xn+1,0),
 3分
3分
 数列
数列 是首项为4 ,公比为
是首项为4 ,公比为 的等比数列
的等比数列  4分
4分
(2)
 数列
数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,且
的等比数列,且 5分
5分
又 ,公比满足
,公比满足 ,
,

 为递减的等比数列,
为递减的等比数列,
∴yn的最大值是y1=x12,
要使得对任意的正整数 都有
都有 恒成立,只要
恒成立,只要 6分
6分
解得 ,又
,又
 ,
, 的最大值为
的最大值为 7分
7分
(3)由(1)得 8分
8分
 ①
①
 ②
②
①-②得

 11分
11分
当 时,
时,
当 时,
时, 12分
12分
当 时,
时,

故Tn>1. 14分

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目